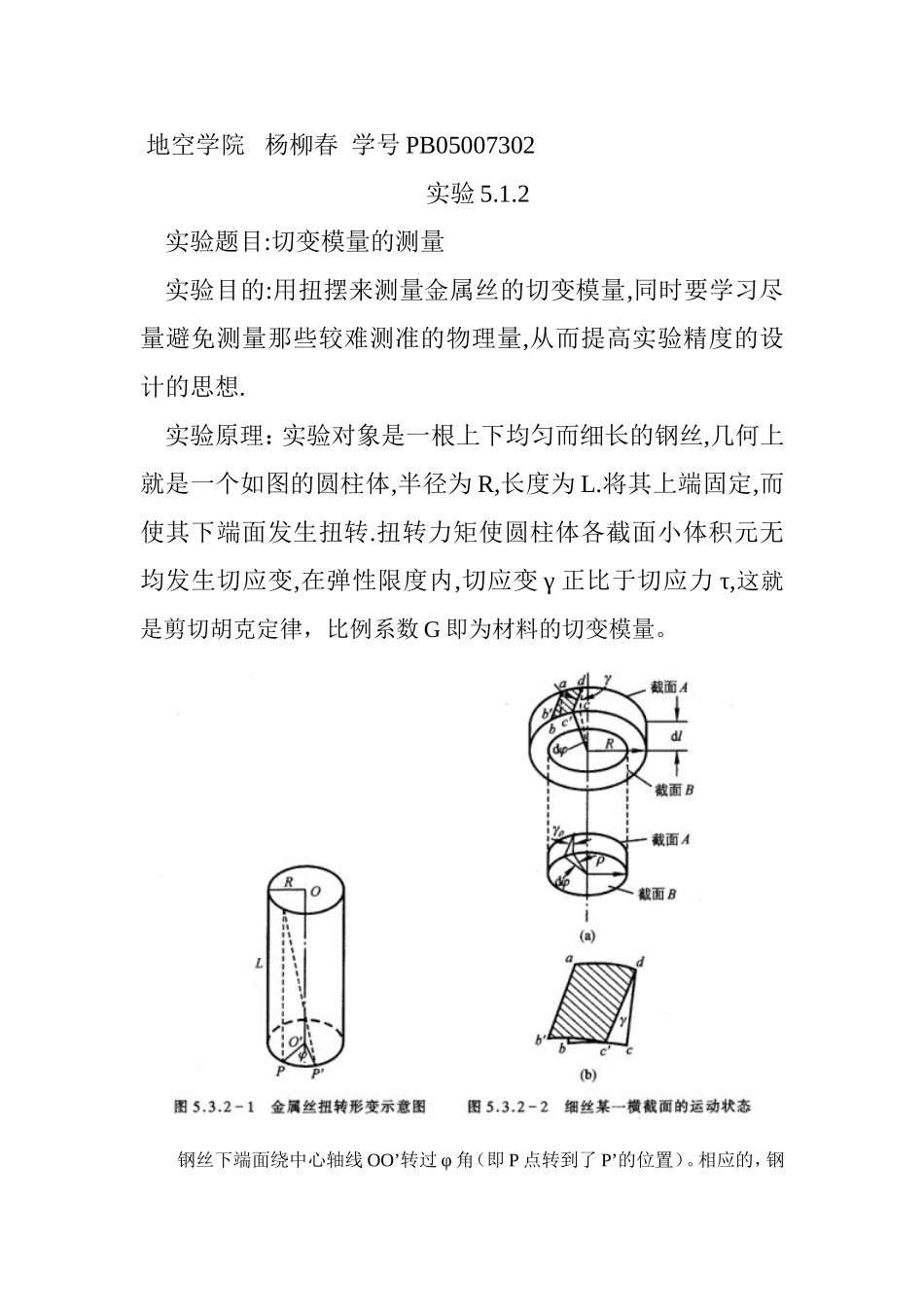
地空学院杨柳春学号PB05007302实验5.1.2实验题目:切变模量的测量实验目的:用扭摆来测量金属丝的切变模量,同时要学习尽量避免测量那些较难测准的物理量,从而提高实验精度的设计的思想.实验原理:实验对象是一根上下均匀而细长的钢丝,几何上就是一个如图的圆柱体,半径为R,长度为L.将其上端固定,而使其下端面发生扭转.扭转力矩使圆柱体各截面小体积元无均发生切应变,在弹性限度内,切应变γ正比于切应力τ,这就是剪切胡克定律,比例系数G即为材料的切变模量。钢丝下端面绕中心轴线OO’转过φ角(即P点转到了P’的位置)。相应的,钢丝各横截面都发生转动,其单位长度的转角。分析这细圆柱中长为的一小段,其上截面为A,下截面为B(如图5.3.2-2所示)。由于发生切变,其侧面上的线ab的下端移至b’,即ab转动了一个角度γ,,即切应变(2)在钢丝内部半径为ρ的位置,其切应变为(3)由剪切胡克定律可得横截面上距轴线OO’为ρ处的切应力。这个切应力产生的恢复力矩为截面A、B之间的圆柱体,其上下截面相对切变引起的恢复力矩M为(4)因钢丝总长为L,总扭转角,所以总恢复力矩(5)所以(6)于是,求切变模量G的问题就转化成求钢丝的扭矩(即其恢复力矩)的问题。为此,在钢丝下端悬挂一圆盘,它可绕中心线自由扭动,成为扭摆。摆扭过的角度φ正比于所受的扭力矩,(7)D为金属丝的扭转模量。将式(7)代入式(6),有(8)由转动定律(9)I0为摆的转动惯量,再由式(7)和(9)可得(10)这是一个简谐运动微分方程,其角频率,周期(11)作为扭摆的圆盘上带有一个夹具,这给测量或计算I0带来困难。为此,可将一个金属环对称地置于圆盘上。设环的质量为m,内外半径分别为r内和r外,转动惯量为,这时扭摆的周期(12)由式(11)、(12)可得(13)(14)(15)测量数据:金属环的质量为:514g;12345平均值标准差线长L(cm)45.0045.0544.9645.0345.0845.020.04128D内(cm)7.9427.9307.9347.9447.9327.9360.0056D外(cm)10.01810.01010.01610.02010.02010.0160.0037t0=50T0(s)112.70112.85112.68112.98112.97112.840.1278t1=50T1(s)171.27171.64171.82171.26171.63171.520.222012345678910平均值直径D(cm)0.7850.7900.7690.7870.7720.7700.7800.7750.7750.7850.779由于千分尺的零刻度的实际示数为-0.001mm,故钢丝的直径的实际平均值为0.789-(-0.001)=0.780mm。所以有下列平均值:R环=0.390mmL=45.02cmR内=3.968cmR外=5.008cmT0=2.26sT1=3.43s数据分...