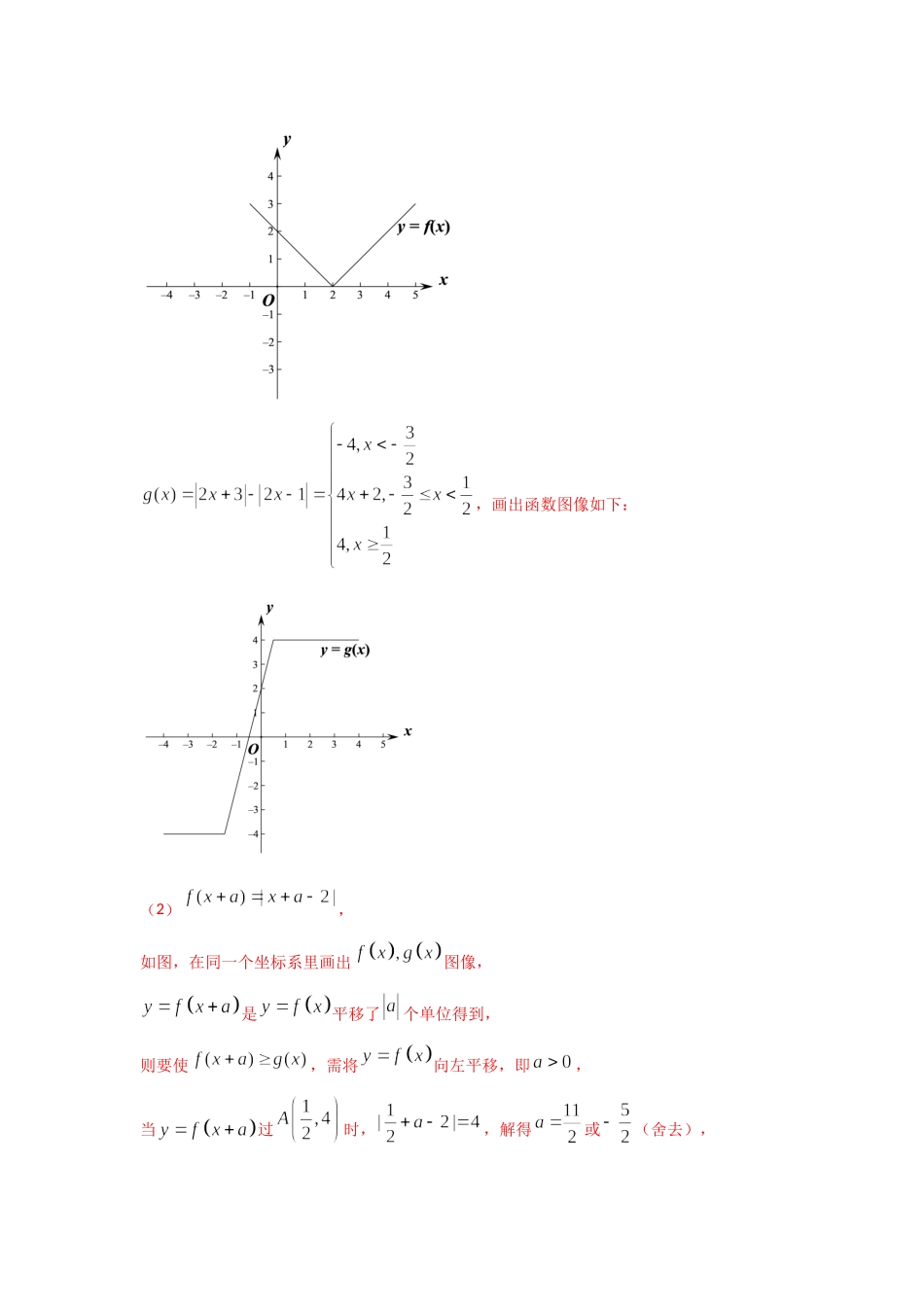
专题19不等式选讲1.【2021年全国高考甲卷数学(理)试题】已知函数.(1)画出和的图像;(2)若,求a的取值范围.【答案】(1)图像见解析;(2)【分析】(1)分段去绝对值即可画出图像;(2)根据函数图像数形结和可得需将向左平移可满足同角,求得过时的值可求.【详解】(1)可得,画出图像如下:,画出函数图像如下:(2),如图,在同一个坐标系里画出图像,是平移了个单位得到,则要使,需将向左平移,即,当过时,,解得或(舍去),则数形结合可得需至少将向左平移个单位,.【点睛】关键点睛:本题考查绝对值不等式的恒成立问题,解题的关键是根据函数图像数形结合求解.2.【2021年全国高考乙卷数学(理)试题】已知函数.(1)当时,求不等式的解集;(2)若,求a的取值范围.【答案】(1).(2).【分析】(1)利用绝对值的几何意义求得不等式的解集.(2)利用绝对值不等式化简,由此求得的取值范围.【详解】(1)当时,,表示数轴上的点到和的距离之和,则表示数轴上的点到和的距离之和不小于,当或时所对应的数轴上的点到所对应的点距离之和等于6,∴数轴上到所对应的点距离之和等于大于等于6得到所对应的坐标的范围是或,所以的解集为.(2)依题意,即恒成立,,当且仅当时取等号,,故,所以或,解得.所以的取值范围是.【点睛】解绝对值不等式的方法有零点分段法、几何意义法.解含有两个绝对值,且其中的的系数相等时,可以考虑利用数轴上绝对值的几何意义求解;利用绝对值三角不等式求最值也是常见的问题,注意表述取等号的条件.3.【2020年高考全国Ⅰ卷理数】[选修4—5:不等式选讲](10分)已知函数.(1)画出的图像;(2)求不等式的解集.【解析】(1)由题设知的图像如图所示.(2)函数的图像向左平移1个单位长度后得到函数的图像.的图像与的图像的交点坐标为.由图像可知当且仅当时,的图像在的图像上方,故不等式的解集为.4.【2020年高考全国II卷理数】[选修4—5:不等式选讲](10分)已知函数f(x)=|x-a2|+|x-2a+1|.(1)当a=2时,求不等式f(x)≥4的解集;(2)若f(x)≥4,求a的取值范围.【解析】(1)当时,因此,不等式的解集为.(2)因为,故当,即时,.所以当a≥3或a≤-1时,.当-1