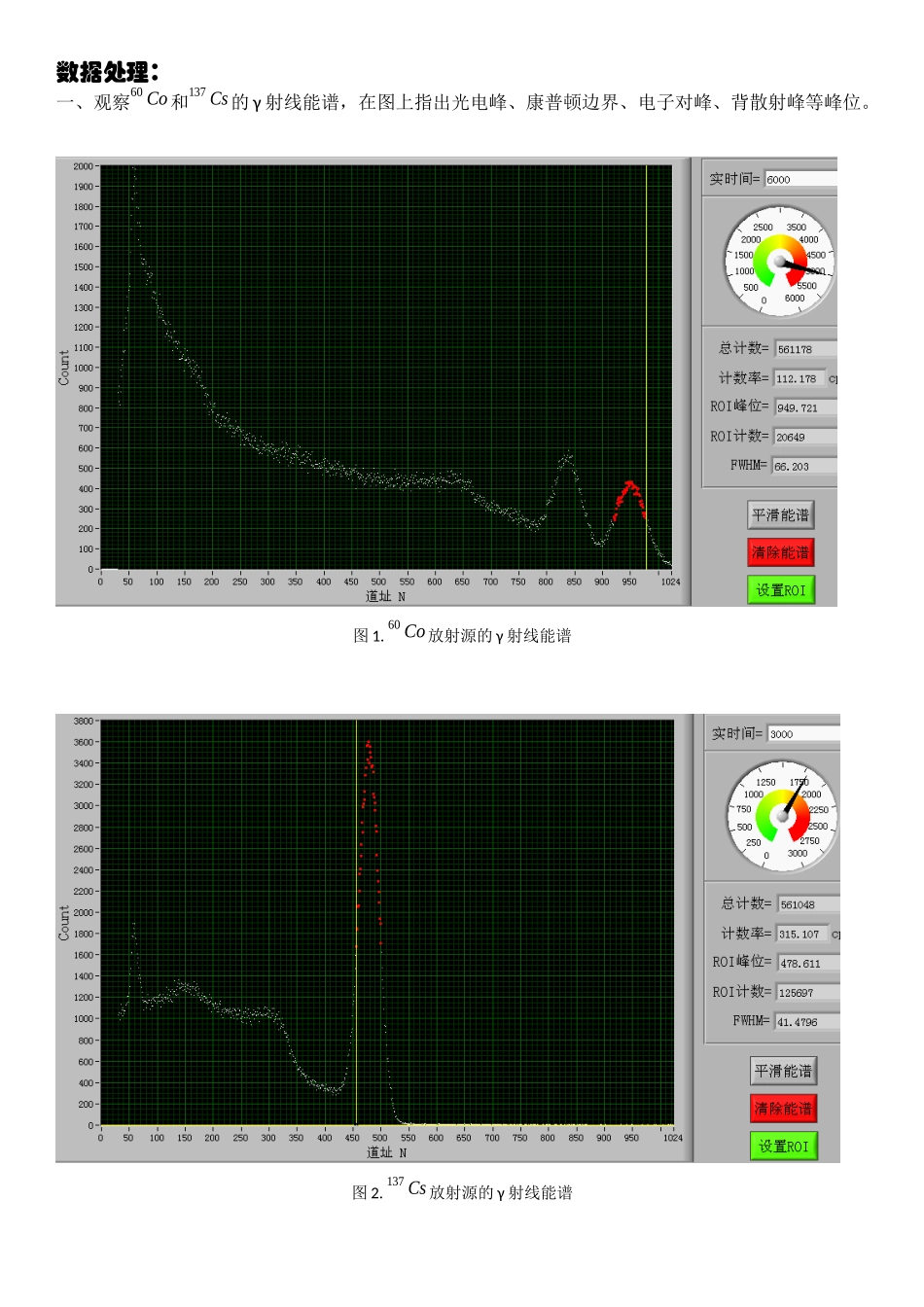
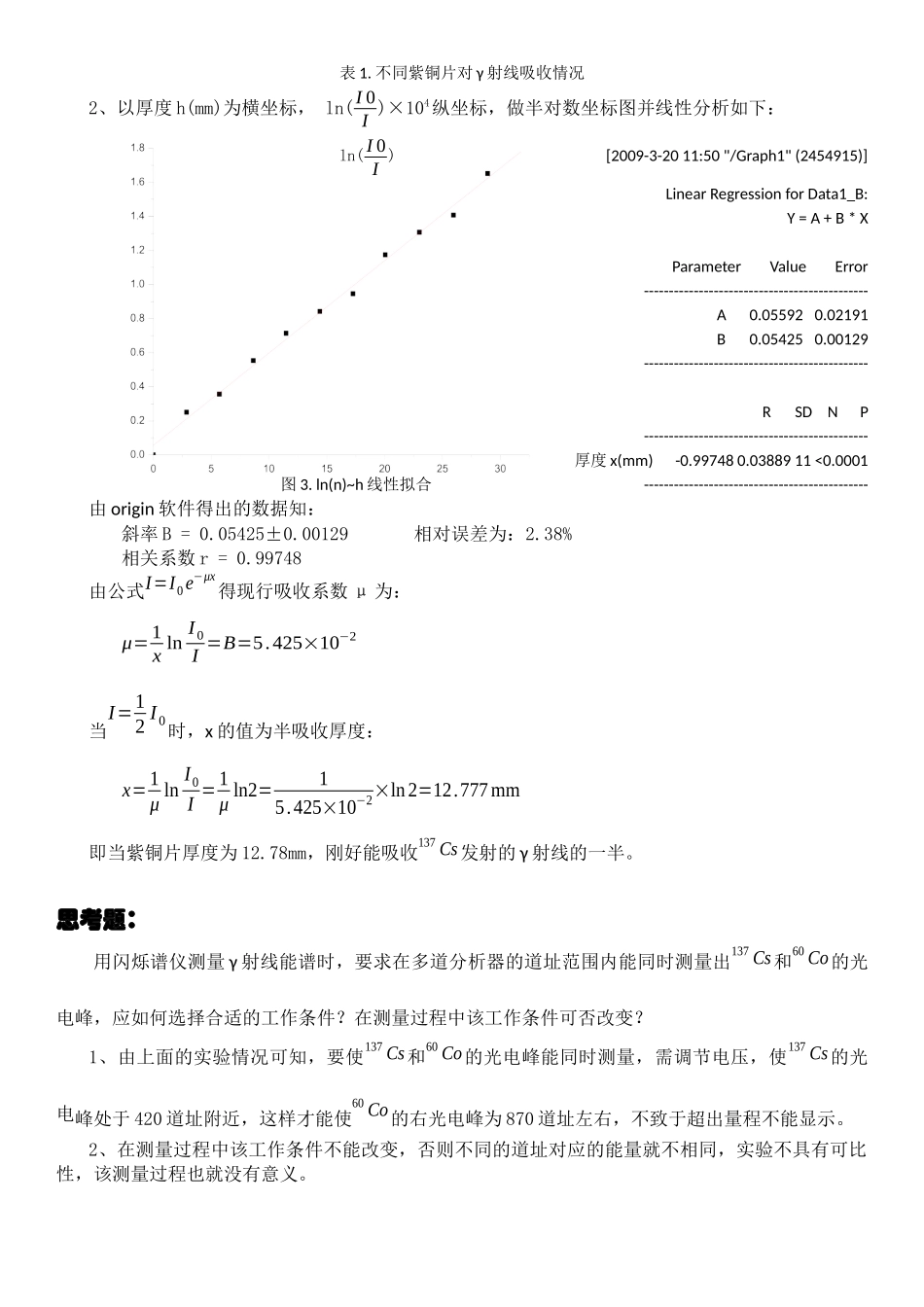
数据处理:一、观察60Co和137Cs的γ射线能谱,在图上指出光电峰、康普顿边界、电子对峰、背散射峰等峰位。图1.60Co放射源的γ射线能谱图2.137Cs放射源的γ射线能谱二、计算137Cs的光电峰和60Co的左侧光电峰对应的能量刻度。已知:60Co的左侧光电峰Eγ1=1.17MeV对应B道,137Cs的光电峰Eγ=0.661MeV对应A道于是可得能量刻度公式为:e=1.17−0.661B−AMeV其中由实验数据可知,B道道址为835.738,由图2知A道道址为478.611。代入数据得:e=1.17−0.661B−AMeV=1.17−0.661835.738−478.611MeV=1.425×10−3MeV三、测量60Co的右侧光电峰能量及计算137Cs光电峰的能量分辨率。1、测量60Co的右侧光电峰能量60Co的右侧光电峰能量=60Co的右侧光电峰道址C×能量刻度e即E2=C×e=949.721×1.425×10−3MeV=1.353MeV≈1.35MeV与理论值Eγ2=1.33MeV相比,相对误差为−¿❑¿×100%=1.50%理论值比实验值少一位有效数字,所以相对误差不大准确。但从中可看出实验误差相对较小,说明实验比较成功,实验较为精确。由于我们选择的60Co放射源不大活跃或是我们4号台的仪器不大灵敏,导致我们组在进行5000多秒后,右侧光电峰的计数才刚到440左右(参见图1)。由于计数的数量不足够大也是造成误差的主要原因之一。2、计算137Cs光电峰的能量分辨率137Cs光电峰的能量分辨率为:η=FWHMEγ×e=FWHMEγ×e=41.47960.661×1.425×10−3×100%=8.94%四、测量紫铜片对137Cs发射的γ射线的吸收曲线,在半对数纸上作图,求出线性吸收系数和半吸收厚度。1、将实验数据制作成表格,如下:(其中I0=36528)铜片个数012345678910厚度x(mm)02.885.728.6411.4814.4017.2620.0623.0025.9428.90CountI3652828447255622100317897157301418211287989089407007ln(I0I)×10400.2500.3570.5530.7130.8420.9461.1741.3061.4081.651表1.不同紫铜片对γ射线吸收情况2、以厚度h(mm)为横坐标,ln(I0I)×104纵坐标,做半对数坐标图并线性分析如下:ln(I0I)[2009-3-2011:50"/Graph1"(2454915)]LinearRegressionforData1_B:Y=A+B*XParameterValueError---------------------------------------------A0.055920.02191B0.054250.00129---------------------------------------------RSDNP---------------------------------------------厚度x(mm)-0.997480.0388911<0.0001图3.ln(n)~h线性拟合---------------------------------------------由origin软件得出的数据知:斜率B=0.05425±0.00129相对误差为:2.3...