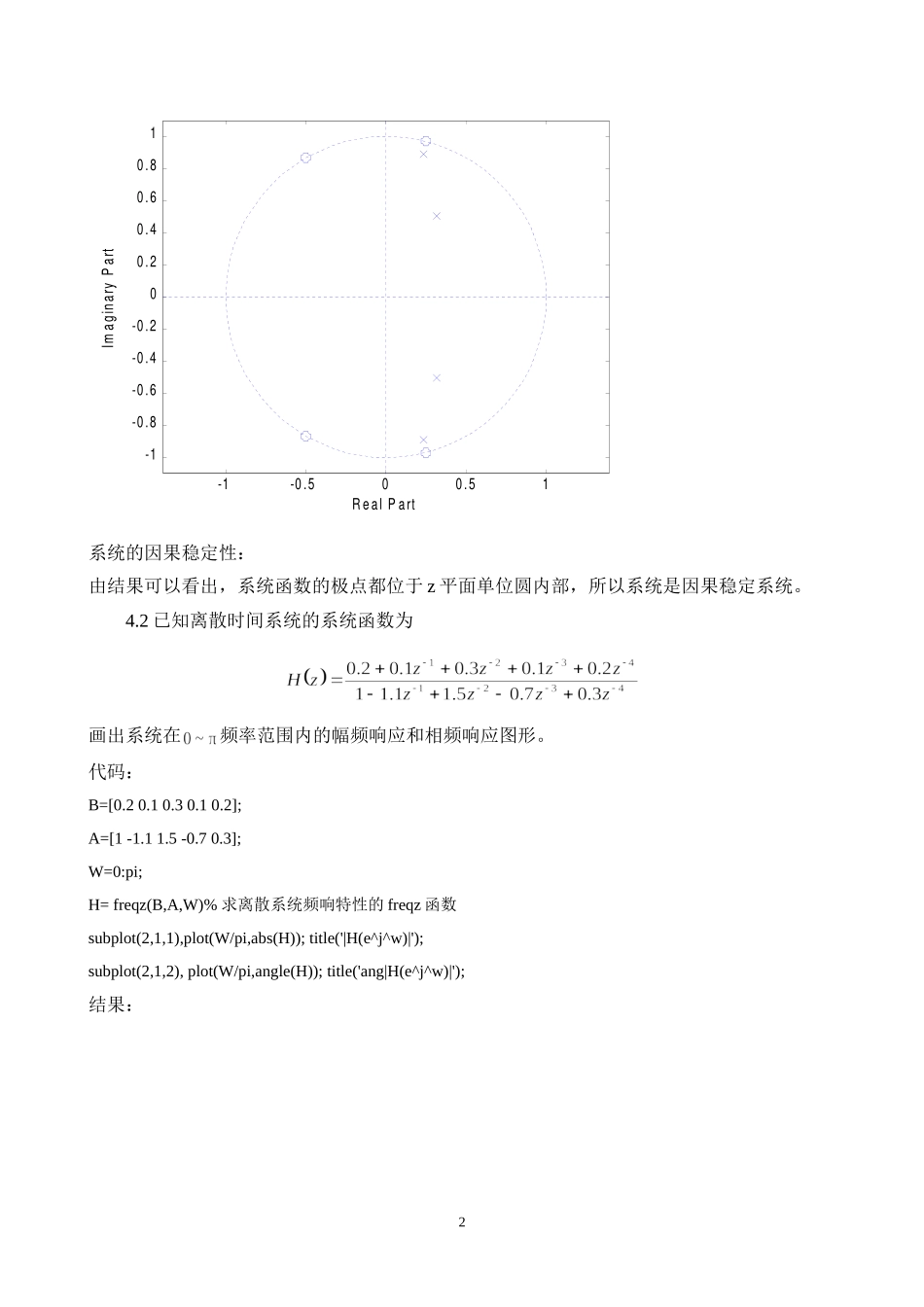
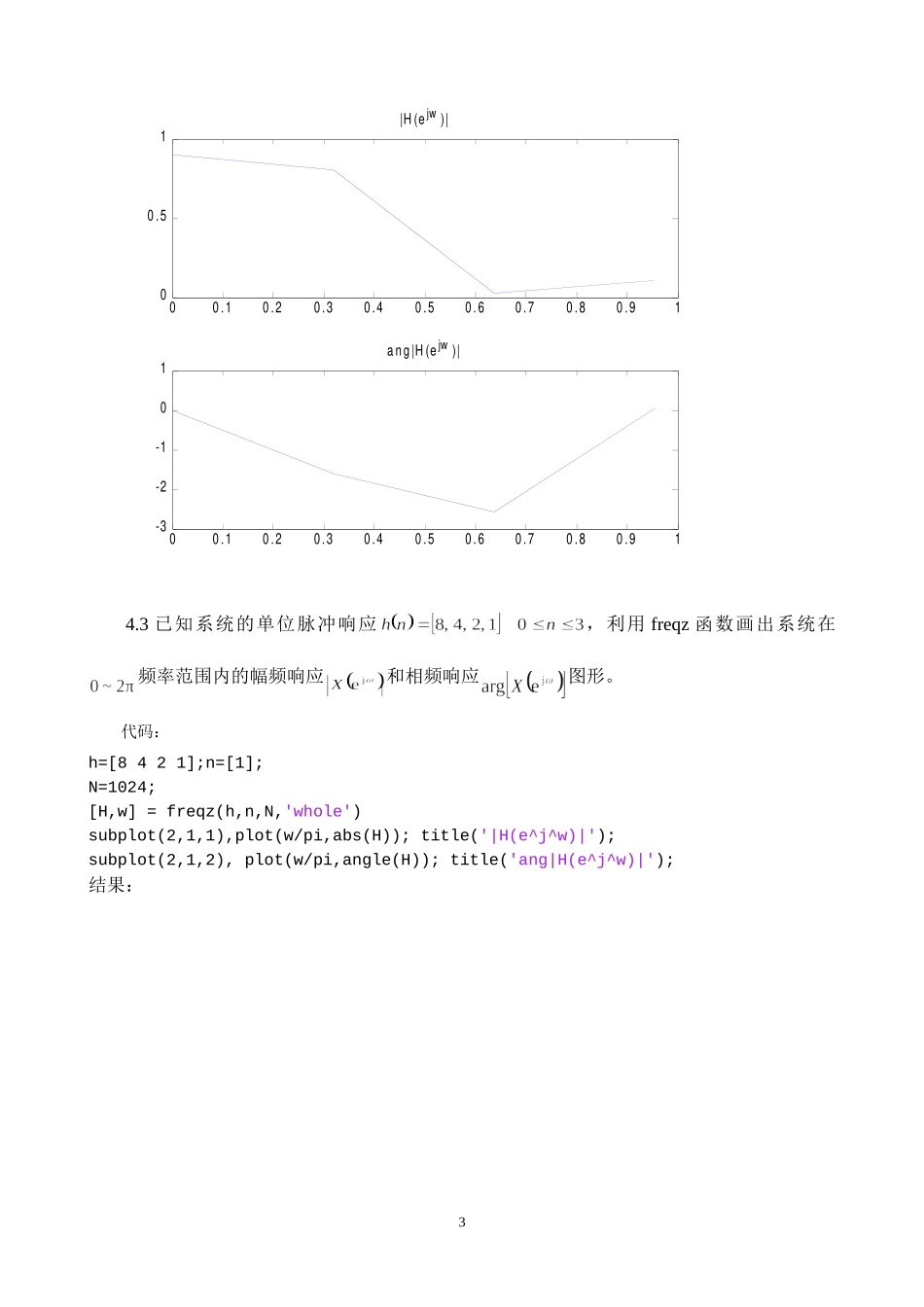
实验4离散时间系统的频域分析15级生物医学工程曹美颖20151507023一、实验目的(1)了解离散系统的零极点与系统因果性和稳定性的关系;(2)加深对离散系统的频率响应特性基本概念的理解;(3)熟悉MATLAB中进行离散系统零极点分析的常用子函数;(4)掌握离散系统幅频响应和相频响应的求解方法。二、实验内容4.1已知离散时间系统的系统函数为求系统的零极点,画出零极点分布图,判断系统的因果稳定性。代码:B=[0.20.10.30.10.2];%B为分子各项系数A=[1-1.11.5-0.70.3];%A为分母各项系数zplane(B,A)结果:零点:-0.5000+0.8660i-0.5000-0.8660i0.2500+0.9682i0.2500-0.9682i极点:0.2367+0.8915i0.2367-0.8915i0.3133+0.5045i0.3133-0.5045i1-1-0.500.51-1-0.8-0.6-0.4-0.200.20.40.60.81RealPartImaginaryPart系统的因果稳定性:由结果可以看出,系统函数的极点都位于z平面单位圆内部,所以系统是因果稳定系统。4.2已知离散时间系统的系统函数为画出系统在频率范围内的幅频响应和相频响应图形。代码:B=[0.20.10.30.10.2];A=[1-1.11.5-0.70.3];W=0:pi;H=freqz(B,A,W)%求离散系统频响特性的freqz函数subplot(2,1,1),plot(W/pi,abs(H));title('|H(e^j^w)|');subplot(2,1,2),plot(W/pi,angle(H));title('ang|H(e^j^w)|');结果:200.10.20.30.40.50.60.70.80.9100.51|H(ejw)|00.10.20.30.40.50.60.70.80.91-3-2-101ang|H(ejw)|4.3已知系统的单位脉冲响应,利用freqz函数画出系统在频率范围内的幅频响应和相频响应图形。代码:h=[8421];n=[1];N=1024;[H,w]=freqz(h,n,N,'whole')subplot(2,1,1),plot(w/pi,abs(H));title('|H(e^j^w)|');subplot(2,1,2),plot(w/pi,angle(H));title('ang|H(e^j^w)|');结果:300.511.5251015|H(ejw)|00.511.52-1-0.500.51ang|H(ejw)|4.4已知离散时间系统的系统函数为画出系统在频率范围内的幅频响应和相频响应图形,并与课本上例2-9进行对比。代码:x=[exp(j*pi/2),exp(-j*pi/2)];B=poly(x);%得到分子多项式的系数x=[0.8*exp(j*pi/4),0.8*exp(-j*pi/4)];A=poly(x);%得到分母多项式的系数[H,w]=freqz(B,A,'whole')subplot(2,1,1),plot(w,abs(H));title('|H(e^j^w)|');subplot(2,1,2),plot(w,angle(H));title('ang|H(e^j^w)|')结果:4012345670246|H(ejw)|01234567-4-2024ang|H(ejw)|4.5已知系统单位脉冲响应为,如果输入为,利用圆周卷积定理求系统输出。代码:n=0:9;xn=exp(0.2.*n);n2=0:19;hn=cos(0.5.*n2)+sin(0.2.*n2);Xk...