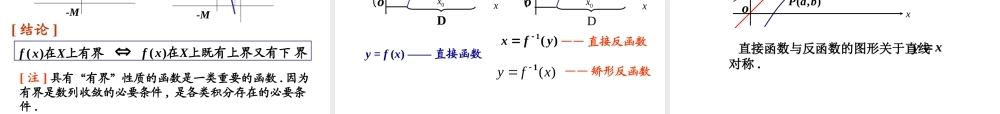第一章(1).pptVIP免费

第一章函数、极限和连续第一节函数函数有界性单调性周期性奇偶性初等函数分段函数复合函数集合映射第一节函数一、函数概念以点a为中心的任何开区间称为点a的邻域,记为U(a).aa+a-U（a,）=（a-,a+）δ>0,称集合(a-δ,a+δ)为点a的δ邻域,记为U(a,δ)..,axxaUaa+a-axx0集合称为点a的去心δ邻域,记为.,aU.0,axxaU即。叫做邻域的半径。叫做邻域的中心；a1、邻域因变量自变量.)(,000处的函数值为函数在点称时当xxfDx.}),({称为函数的值域函数值全体组成的数集DxxfyyW变量y按照一定法则总有确定的数值和它对应，则称y是x的函数，记作定义设x和y是两个变量,D是一个给定的数集，数集D叫做这个函数的定义域)(xfy如果对于每个数Dx,2、函数的定义(())0x)(0xf自变量因变量对应法则f函数的两要素:定义域与对应法则.xyDW约定:定义域是自变量所能取的使算式有意义的一切实数值.21xy例如，]1,1[:D211xy例如，)1,1(:D定义:.)(}),(),{(的图形函数称为点集xfyDxxfyyxCoxy),(yxxyWD如果自变量在定义域内任取一个数值时，对应的函数值总是只有一个，这种函数叫做单值函数，否则叫与多值函数．．例如，222ayx3、函数的表示法解析法：用解析表达式表示函数关系表格法：用列表的方法来表示函数关系图示法：用平面直角坐标系上的曲线来表示函数关系(1)符号函数010001sgnxxxxy当当当几个特殊的函数举例1-1xyoxxxsgn(2)取整函数y=[x][x]表示不超过的最大整数12345-2-4-4-3-2-14321-1-3xyo阶梯曲线x是无理数时当是有理数时当xxxDy01)(有理数点无理数点•1xyo(3)狄利克雷函数(4)取最值函数)}(),(max{xgxfy)}(),(min{xgxfyyxo)(xf)(xgyxo)(xf)(xg0,10,12)(,2xxxxxf例如12xy12xy在自变量的不同变化范围中,对应法则用不同的式子来表示的函数,称为分段函数.•显函数：函数关系用解析式表示的称为显函数，如.•分段函数：有些函数，对于其定义域内自变量的不同值，函数不能用一个统一的公式表示，而要用两个或两个以上的公式来表示，这类函数称为分段函数.•隐函数：函数与自变量的对应法则用一个方程表示的函数，如.()yfx2,lgyxyx2210xyy(,)0Fxy0,10,12)(,2xxxxxf例如12xy12xyxx4、显函数，分段函数，隐函数二、函数的性质1．函数的单调性,,)(DIDxf区...