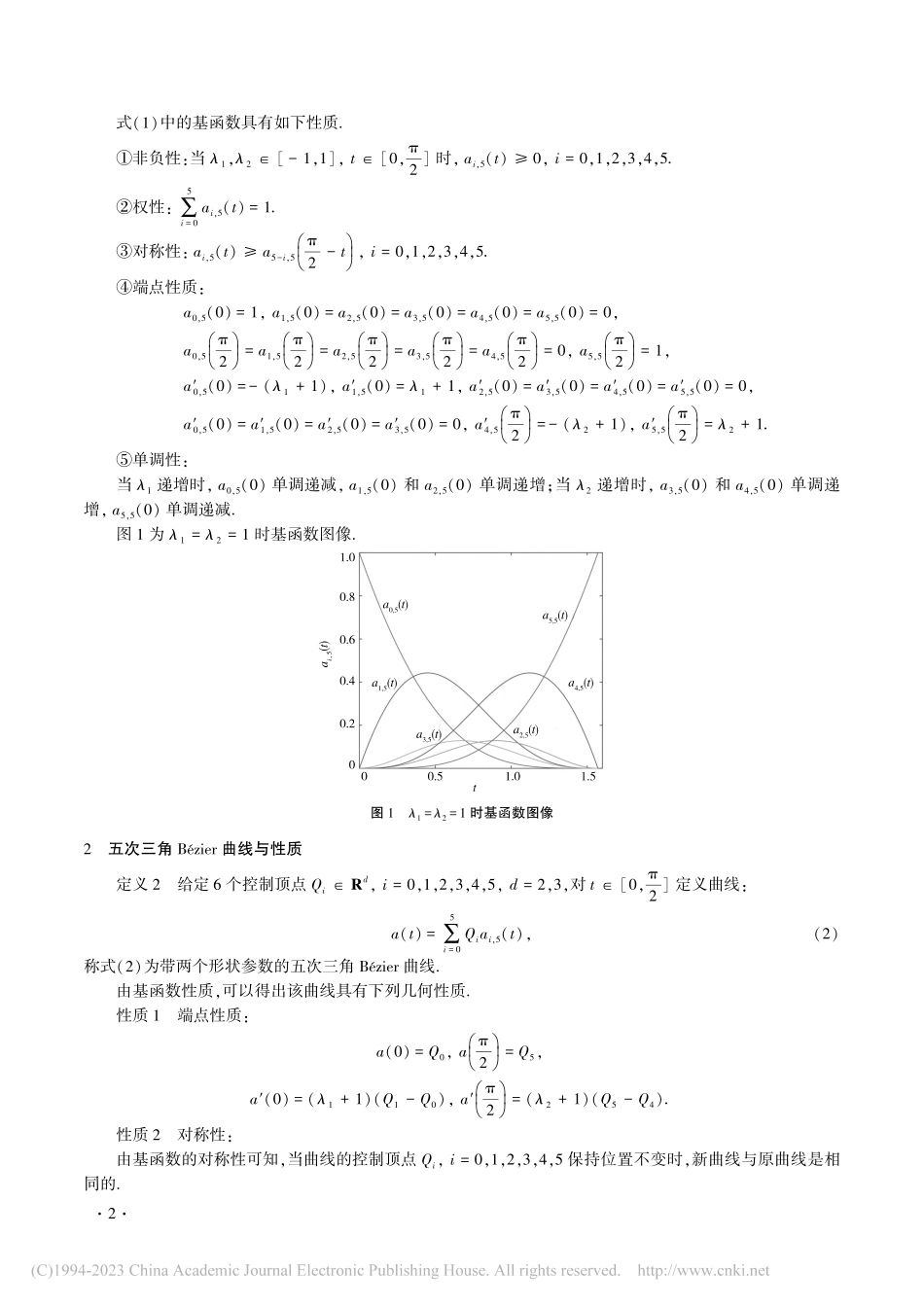
带两个形状参数的五次三角Bézier曲线张丹丹(安徽开放大学安庆分校,安徽安庆246001)[摘要]给出一组带两个形状参数λ1,λ2的五次三角基函数,基于此基函数定义了带两个形状参数的五次三角Bézier曲线.得到的新曲线不仅有Bézier曲线的几何特性,而且还可以对曲线造型进行自由的调整,并且分析了形状参数的几何意义,讨论了曲线间的C1,C2光滑拼接条件.所得曲线能精确地表示椭圆弧和抛物线弧.[关键词]三角Bézier曲线;形状参数;曲线设计;连续[中图分类号]O24[文献标志码]A[文章编号]2095-7602(2023)02-0001-050引言在计算机辅助几何设计(CAGD)中曲线曲面是重要的研究问题.其中,Bézier曲线、B样条曲线[1-2]因其自身的良好性质在工业设计中被广泛应用.但是,曲线形状不能被灵活修改,并且不能精确地表示一些二次曲线.虽然非均匀有理B样条(NURBS)解决了这些问题,但在实际中应用该方法求积、求导计算过程极其复杂.为更好地满足需求,研究者在三角函数空间中找出新的构造方法.ZHANG[3]基于函数空间1,t,cost,sint{}生成了著名的C-曲线,它具有Bézier曲线类似的几何特性,并能精确地表示圆弧曲线.HAN[4-5]分别定义了带参数的二次、三次三角曲线,能够对曲线的形状进行调整,并能精确地表示二次曲线.吴晓勤等[6]分析了带参数的二次三角Bézier曲线,并且讨论了两曲线间的G2和C3拼接.杨联强等[7]研究了带参数的三次三角Bézier曲线,这些曲线能精确地表示椭圆弧和抛物线弧.李军成等[8]讨论了带两个形状参数的类三次三角Bézier曲线,给出了曲线间的C1,C2光滑拼接条件,当选取适当的形状参数时,曲线段可在连接点达到C3拼接.喻德生等[9]定义了四次三角Bézier曲线,给出了两曲线间的C1,C2连续条件,并讨论了其在实际中的应用.本文构造了带两个形状参数λ1,λ2的五次三角Bézier曲线,调整参数λ1,λ2取值,能对曲线的形状进行调控,并给出了两段曲线间的C1,C2光滑拼接条件,该曲线能够精确地表示椭圆弧和抛物线弧.1基函数定义1当λ1,λ2∈[-1,1],t∈[0,π2],t∈R,关于t的函数:a0,5(t)=(1-sint)(1-λ1sint),a1,5(t)=(λ1+1)sintcost(1-sin...