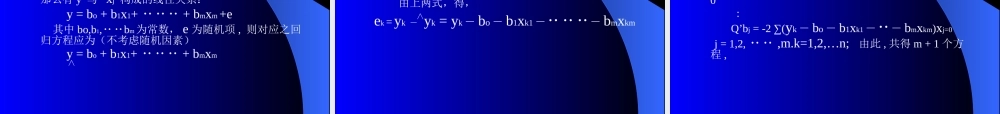回归分析预测法回归分析预测法从本章起将讨论定量预测技术第三章的基本思路来源于数学分析中数理统计的回归分析方法,将因素之间的规律(利用已知统计资料)设为按一定数学模型变化的运动轨迹,并假定:未来的变化仍然是在已知的条件下进行,运动轨迹将不会发生畸变。第一节回归分析的基本概念第一节回归分析的基本概念一.基本概念1.回归分析的来由:20世纪初,英统计学家F.Golden研究父子身高的遗传统计,高个子父母下一代比父亲更高的概率小于比他矮的概率,而矮个子父亲下一代比父亲高的概率大于比他矮的概率;且这两种高度父辈的后代,高度有向两种父辈平均身高靠拢的趋势,这种现象称为“回归”——是一种自然界现象规律的提取。2.回归分析研究变量之间的互相关系,把其中一些因素作为控制的变量,而把另一些随机变量作为因变量,利用适当的数学模型尽可能趋向于趋势变化的均值描述它们的关系的分析,称为回归分析。即假定y与x相关,应有y=f(x)若x1,x2,‥‥‥xn个变量影响y,应有y=f(x1,x2,‥‥‥xn)显然,有一些问题必须解决①因素分析现代社会中,任何一件事物与多个因素相关,如何选取主要因素,忽略次要因素,使建立的数学模型不因变量太多而复杂,又能较好的抓住主要矛盾。解决方法是求相关系数R②运动轨迹的模型主要利用已知统计数据在图上打点进行观察分析,寻求一条最佳线路。采用最小二乘法,即在满足该条线路的模拟值与真值总平方误差∑ei2为最小的条件下,来求出模拟数学模型各参数。(为Gauss--Markov最佳线性与无偏估计量)③相关性检验目的是鉴别所求出的模型是否可靠,方法:利用相关性检验准则进行检验④精确度:即讨论在一定置信度条件下的置信区间⑤预测:前面的问题已解决,数学模型已经建立且可靠,精度问题也已解决,利用延续性原则代入需预测的数据,并求出结果。二.方法分类线性线性一元多元非线性非线性第二节一元线性回归预测第二节一元线性回归预测一.回归方程的建立假定需预测的目标为y,与之对应的因素x,随机抽样,子样数为n,通过图上打点作粗略估计已知的一组对应数据,初步定为线性关系,同时再考虑到随机因素,应有:yi=a+bxi+eii=1,2,……n(1)不考虑随机因素,应有:yi=a+bxii=1,2,n(2)代(2)入(1),求得随机项ei=yi–yi=yi–(a+bxi)(3)ei称为残差∧∧这表示,真值与模拟直线y=a+bx之间存在实际误差ei,累积平方误差为Q=∑ei2,称残差平方和,又称剩余平方和。反之,我们已知的是实际数据(xi,yi),从可...