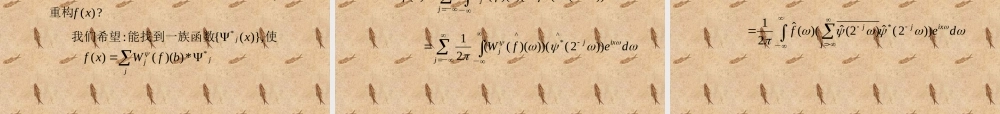二进小波变换.pptVIP免费

二进小波变换－－－－对连续小波变换的频域抽样连续小波变换的缺点：t)(tf空间中一维信号被变换到二维二进小波的基本思想：连续小波变换将一维信号变换到二维变换域上，从而有大量的信息冗余量。的信息。口中包含了一个时频空间窗fabfW),)((),)((00abfW),)((11abfW抽样方法的思考：为完成对频域的分割，应对时间刻度a抽样，其准则为：a)方法简单，高效。b)保留f(t)的全部信息。抽样方法的分析：对频域的分割必须是不重叠，完全的。ZjjA),0(.1jiAAji.2抽样方法的分析：窗口的宽度与其中心频率相适应。（二进制划分）]2,2(),0(ˆ1ˆjjj即),)((1jabfW),)((jabfW),)((1jabfWt抽样方法的分析：问题：怎样确定时间刻度参数a的样本值{aj},使：]2,2(]1,1(ˆ1ˆˆ*ˆ*jjjjjjaaaa抽样方法的分析：]4,2(]1,1(ˆˆˆ*ˆ*jjjjjjaaaaaaˆ*3:我们可以假设的基本性质。而不影响的频率中心可以移动，由于抽样方法的分析：]2,2(]4,2(]1,1(2ˆ1ˆˆˆˆ*ˆ*)1(jjjjjjjjjjaaaaaaa＝则取：二进小波的定义：几乎处处成立使在两个常数，称为二进小波。若存函数BALj22)2(ˆ:,BA00的稳定性条件。这个条件称为二进小波二进小波变换的定义：)21,)((2))((2jjjbfWbfWdtbttfjj))(2()(22))(2(2,2btfjjjj＝其中二进小波稳定性条件的另一种表述：2222LffBfWfAj定理：是一个基小波。即：）（）（满足：条件，则满足二进小波的稳定性令2lnˆ,ˆ2ln0202BddA2lnA2ˆC2＝）（＝时，有：当－dBA定理的证明：BAj2)2(ˆ由稳定性条件：)0()2(ˆ2BAj2121221)2(ˆdBddAj定理的证明：2ln)(ˆ2ln02BdA上积分，可得到：除并在（同样，用)1,22ln)(ˆ2ln02BdA定理的证明：合并上面两式，d2)(ˆ二进小波的重构问题：?)()})(({)})(({)(xfbfWbfWxfjj重构种方法，由反过来，是否能存在一。由二进小波，jjjjbfWxfx***))(()()},({:使能找到一族函数我们希望二进小波的重构问题...