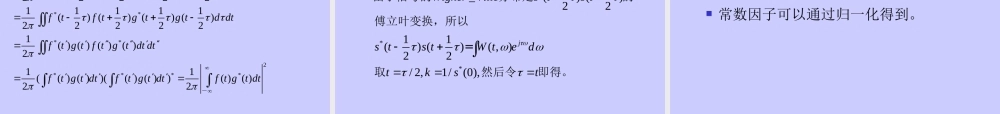Wigner_Ville分布.pptVIP免费

Wigner_Ville分布定义：*(),111(,)()()222jstWignerVilleWtststed对信号其分布定义为：*111()()222jtssedWigner_Ville分布的特性分析：Wigner_Ville分布总是实的，即使s(t)是复信号（实性）。****111(,)()()222111()()222111()()(,)222jjjWtststedststedststedWt因为：对称性：对实信号，有*(,)(,)ˆ(),()()WtWtstss因为：对实信号边缘特性：Wigner_Ville分布满足时频边缘特性。22(1)(,)|()|ˆ(2)(,)|()|WtdstWtdts22(,)|()|ˆ|()|EWtdtdstdtsd＝证明：**2()(,)111()()22211()()()22|()|jPtWtdststeddststdst＝时移频移特性：0000()()(,)(,)jtstesttWtWtt若则000(/2)(/2)*00()*0000(,)111()()222111()()222(,)shjtjtjjWtesttesttedsttsttedWtt证明：函数平均值：Wigner_Ville分布满足边缘特性，所以，函数平均值只是时间和频率的函数。12122212(,)(,)(,)()()(()())(,)ˆ()|()|()|()|gtgtWtdtdgtggtgWtdtdgtstdtgsd＝推论：可以通过Wigner_Ville分布正确计算信号的平均时间、中心频率、持续时间和带宽。可以通过Wigner_Ville分布计算信号的时宽和带宽满足不确定性原理。协方差：2(,)()|()|ttWtdtdttstdt＝局部平均值：221(,)|()|1(,)ˆ|()|()()ttWtdstttWtdstt时间和频率的一阶条件矩是可以得到局部带宽：22222222|21(,)|()|1()()[()()]()2()()1()()[()()]2()()ttttWtdstAtAttAtAtAtAtAtAt频率的二阶条件矩是可以得到例：正弦波和冲激0000()(,)()()()(,)()jtsteWtstttWttt例：具有高斯包络的正弦波202201/4/2()/()()1(,)jtttasteeWtee例：线性调频信号20/20()(,)()jtjtsteWttWigner_Ville分布的支撑：0000_,(,),WignerVilletWtt分布可以精确的定...