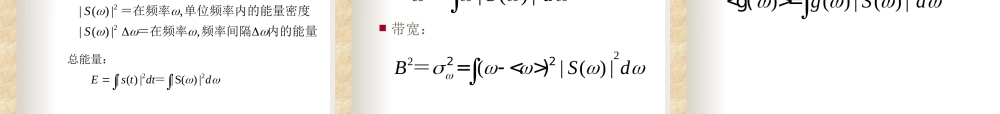Fourier分析简介.pptVIP免费

Fourier分析简介——概念与基本性质Fourier变换的定义：RtiRtideftfFourierdtetff)(ˆ21)(ˆ)()(ˆ变换：逆其中：1.f(t)在任意区间满足狄里克雷条件。2.f(t)绝对可积。)()(ˆ)(tftftf的连续点，有在Fourier变换的物理意义：Fourier变换的基本性质：线性性对称性共轭性ˆ(()())()()axtbytaxbyˆˆ(())2()xtxtˆˆ(())()()xtx)(ˆ1)(axaatx时间展缩性：)(ˆ)(xtx翻卷性：)(ˆ00)(xetittx时移性：)(ˆ00))((xtjtxe频移性：)(ˆ)()(^)(xitxnn微分性：)(ˆ)()()(^nnxtxit频率微分性：dttxtmmixnnnnn)())0(ˆ)()(其中：＝（矩量公式：0)(ˆlimx频率极限：dxxgxtftgfgfgf)()())(*(ˆˆ)*(^其中：卷积定理：Fourier变换的基本定理：ikxkikxecxfxfLZxe21)(L)(]2,0[}21{22，有：即：对任意的的规范正交基。构成函数族定理1：Fourier变换的基本定理：定理2（Pavseval恒等式）：22122ˆ2,2ˆ,ˆ,,ffgfgfLgf－）（特别有：有Fourier变换的基本定理：定理3（Poisson定理）：－－－－则：处处收敛。级数数。处处收敛与某个连续函周期延拓绝对可积，且满足若ikxikxekfkxfekfFourierkxfxf)(ˆ21)2()(ˆ21.2)2(.1)(例子：高斯函数的Fourier变换仍是高斯函数。aaxeafaexf422)(ˆ0)(则：证明：dxeyfxyax2)(令dxeayayxa4)2(22dxeeaxay2241＝利用dxex2aeaiy42,－则原式＝令信号的基本特征：信号的时域描述22|()|,|()|,sttstttt能量密度：＝在时间单位时间内的能量密度＝在时间时间间隔内的能量2|()|Estdt总能量：信号波形的时域特征：平均时间（时间中心）：2|()|ttstdt<>=持续时间(时宽）：2(|()|ttstdt22t=<>)任意时间函数的平均值：2)()|()|tgtstdt=例：高斯（Gauss）包络信号：20()()1/42()(/)0attjtstea20()1/20(/)attttedtt平均时间：例：22212ttta20()21/22201(/)2attttedtta持续时间信号的基本特征：信号的频域描述22|()|,|()|,SS频谱能量密度：＝在频率单位频率内的能量密度＝在频率频率间隔内的能量...