趋势曲线模型预测76ezj.pptVIP免费

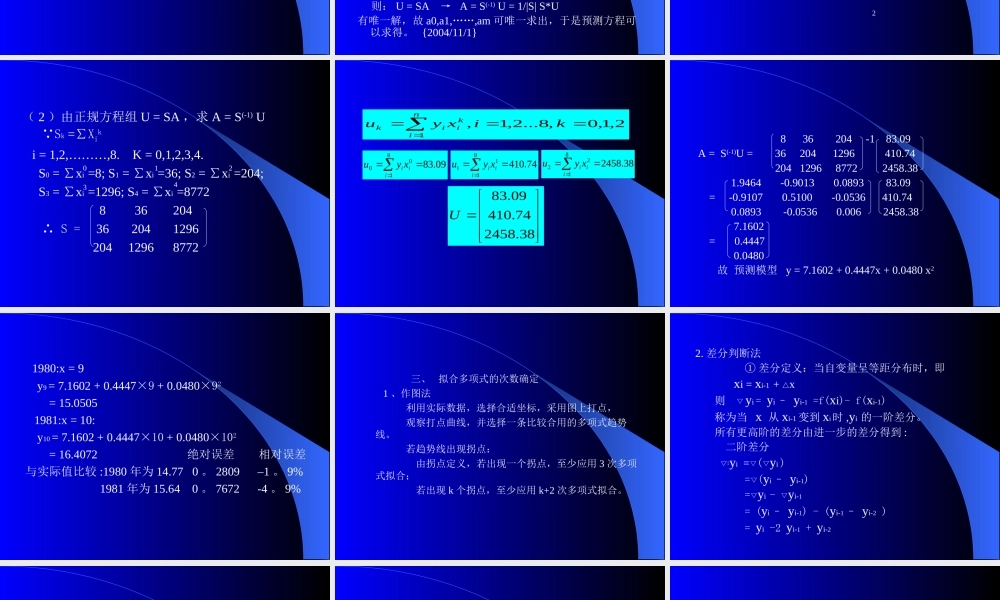
趋势曲线模型预测趋势曲线模型预测第一节第一节多次式曲线模型预测多次式曲线模型预测法法第三章所谈及的回归分析，是在已知统计资料基础上，利用线性或非线性回归技术进行模拟，利用趋势外推进行预测，而模型的项数均为常数项加一次项或非线性构成。事实上，若采用多项式进行模拟，也是一种行之有效的方法。一．正规方程组所谓多项式回归，就是已知统计资料给出，当预测变量y与自变量x可用一个多项式进行模拟时，利用一元非线性回归技术，来作出模拟并用于预测。设实际值为（xi,yi）,为方便多项式次数测定，数据选取xi－xi－1=∆x=C，模型模拟值为(xi,)就有=f(x)=a0+a1x+a2x+……+amx.显然，这是一个m次多项式，同时假定已知数据为n组：(xi,yi)i=1,2,……n.2mni1iyˆiyˆ假定y与x是相关的，对应任意的yi，都有yi且ei=yi－由回归分析，最佳拟合为Q=∑ei2=Qmin利用最小二乘法，对系数求偏导数，有(Q/ak)’=0→2∑ei(ei)’ak=0其中k=0,1,2,3,……,m因为ei=yi－yi=yi－a0－a1x－……akxik……amxim所以有：∑(yi－a0－a1x1--……amxim)(-xik)=0得yixik=a0∑xik+a1∑xi(k+1)+……am∑xik+miyˆni1ni1令nikiikxyu1,tbatKynikikxs1可建立m+1个方程组成的正规方程组：s0a0+s1a1+……+smam=u0(k=0)s1a0+s2a1+………+sm+1am=u1(k=1)::::sma0+sm+1a1+……..+s2mam=um(k=m)记为矩阵式：s0s1s2……sma0u0s1s2s3……sm+1a1u2smsm+1s0…s2mamum记为S记为A记为U则：U=SA→A=S(-1)U=1/|S|S*U有唯一解，故a0,a1,……,am可唯一求出，于是预测方程可以求得。{2004/11/1}=×二、案例某地1972---1979工业产值统计资料如表，企业多项式模型，并预测1980、1981年工业产值年19721973197419751976197719781979序号12345678产值7.548.768.239.9210.6511.6512.5613.78解：（1）描点，观察，做趋势图。由图所示，用二次曲线描述合理。即预测模型可取为y=a0+a1x+a2x2（2）由正规方程组U=SA，求A=S(-1)U Sk=∑Xiki=1,2,………,8.K=0,1,2,3,4.S0=∑xi=8;S1=∑xi=36;S2=∑xi=204;S3=∑xi=1296;S4=∑xi=8772836204∴S=36204129620412968772012342,1,0,8...2,1,1kixyunikiik09.838100iiixyu74.4108111iiixyu38.24588122iiixyu38.245874.41009.83U836204-183.09A=S(-1)U=362041296410.74204129687722458.381.9464-0.90130.089383.09=-0.91070.5100-0.0536410.740.0893-0.05360.0062458.387....