初中数学教学课件：14.2.2完全平方公式(第1课时)（人教版八年级上）.pptVIP免费

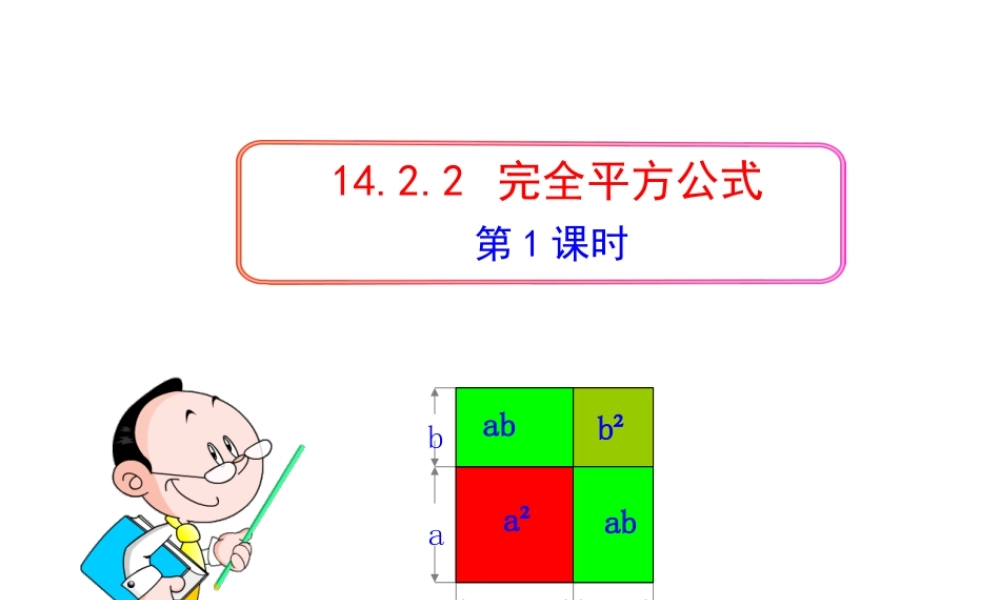
第1课时14.2.2完全平方公式bbaa(a+b)²a²b²abab1.经历完全平方公式的推导过程、几何解释，进一步发展符号感和推理能力．2.理解完全平方公式的结构特征并能灵活应用公式进行计算．a2b2一位老人非常喜欢孩子．每当有孩子到他家做客时，老人都要拿出糖果招待他们．来一个孩子，老人就给这个孩子一块糖，来两个孩子，老人就给每个孩子两块塘，…（1）第一天有a个男孩去了老人家，老人一共给了这些孩子多少块糖？（2）第二天有b个女孩去了老人家，老人一共给了这些孩子多少块糖？（3）第三天这（a+b）个孩子一起去看老人，老人一共给了这些孩子多少块糖？（4）这些孩子第三天得到的糖果数与前两天他们得到的糖果总数哪个多？多多少？（a+b）2（a+b）2-（a2+b2）（a+b）2-（a2+b2）我们上一节学习了平方差公式即(a+b)(a-b)=a2-b2，现在遇到了两个数的和的平方，即(a+b)2，这是我们这节课来研究的新问题．计算下列各式,你能发现什么规律?(1)(p+1)2=(p+1)(p+1)=_________;(2)(m+2)2=_________;(3)(p-1)2=(p-1)(p-1)=________;(4)(m-2)2=__________.p2+2p+1m2+4m+4p2-2p+1m2-4m+4（5）计算(a+b)2,(a-b)2.【解析】(a+b)2=(a+b)(a+b)=a2+ab+ab+b2=a2+2ab+b2.(a-b)2=(a-b)(a-b)=a2-ab-ab+b2=a2-2ab+b2完全平方公式:(a+b)2a+2ab+b22=(a-b)2a-2ab+b22=两个数的和（或差）的平方，等于它们的平方和，加上（或减去）它们的积的2倍.公式的特点：4.公式中的字母a，b可以表示数，单项式和多项式.(a+b)2=a2+2ab+b2(a-b)2=a2-2ab+b21.积为二次三项式；2.其中两项为两数的平方和；3.另一项是两数积的2倍，且与乘式中间的符号相同.首平方，尾平方，积的2倍在中央bbaa2)(baa²2ab²2bababab2++完全平方和公式：aabb2)(ba2aab222aabba²ababab2bb²bb完全平方差公式：【例1】运用完全平方公式计算：【解析】(x+2y)2==x2(1)(x+2y)2(a+b)2=a2+2ab+b2x2+2•x•2y+(2y)2+4xy+4y2(2)(-a2+b3)2【解析】原式=(b3-a2)2=b6-2a2b3+a4 (a-b)2=(b-a)2∴(-a2+b3)2=(a2-b3)2【例2】运用完全平方公式计算:(1)1022;(2)992.【解析】(1)1022=(100+2)2=1002+2×100×2+22=10000+400+4=10404(2)992=(100-1)2=1002-2×100×1+12=10000-200+1=98011.下面各式的计算结果是否正确？如果不正确，应当怎样改正？错错错错(x+y)2=x2+2xy+y2(x-y)2=x2-2xy+y2(x-y)2=x2--2xy+y2(x+y)2=x2+22xy+y2(1)(x+y)2=x2+y2(2)(x-y)2=x2-y2(3)(x-y)2=x2+2xy+y2(4)(x+y)2=x2+xy+y2(1)(6a+5b)2=36...