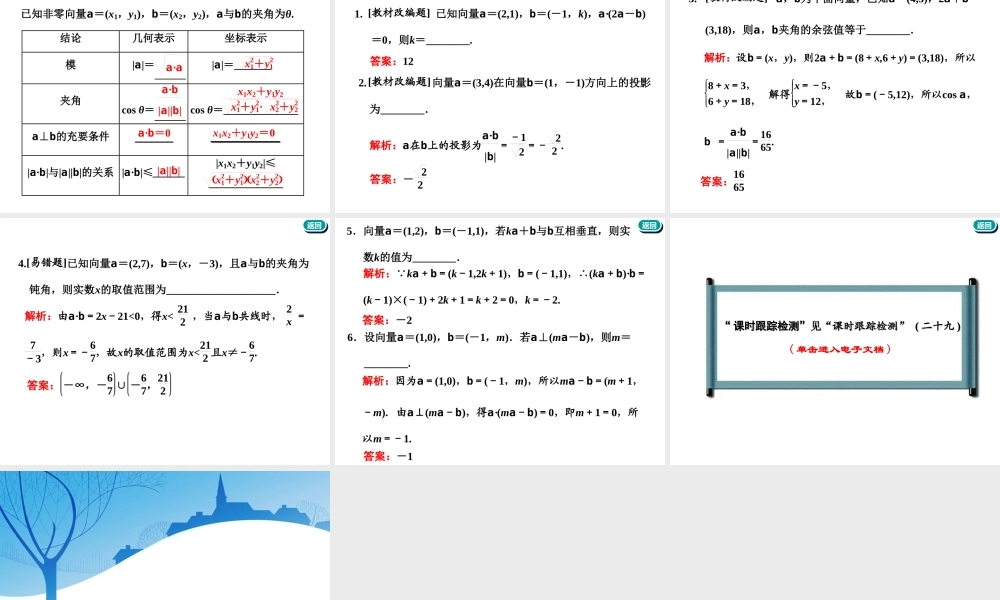
第三节平面向量的数量积及其应用[考纲要求]1.理解平面向量数量积的含义及其物理意义.了解平面向量的数量积与向量投影的关系.2.掌握数量积的坐标表达式,会进行平面向量数量积的运算.3.能运用数量积表示两个向量的夹角,会用数量积判断两个平面向量的垂直关系.4.会用向量方法解决某些简单的平面几何问题.会用向量方法解决简单的力学问题与其他一些实际问题.123Contents知识点一平面向量的数量积知识点二平面向量数量积的坐标表示课时跟踪检测第1课时系统知识——平面向量的数量积返回返回1.向量的夹角(1)定义:已知两个非零向量a和b,作OA―→=a,OB―→=b,则就是向量a与b的夹角.(2)范围:设θ是向量a与b的夹角,则0°≤θ≤180°.(3)共线与垂直:若θ=0°,则a与b;若θ=180°,则a与b;若θ=90°,则a与b.∠AOB同向垂直反向平面向量的数量积返回返回2.平面向量的数量积(1)定义:已知两个非零向量a与b,它们的夹角为θ,则数量____________叫做a与b的数量积(或内积),记作a·b,即a·b=|a||b|cosθ,规定零向量与任一向量的数量积为0,即0·a=0.(2)几何意义:数量积a·b等于a的长度|a|与b在a的方向上的投影_________的乘积.|a||b|cosθ|b|cosθ返回返回[提醒](1)数量积a·b也等于b的长度|b|与a在b方向上的投影|a|cosθ的乘积,这两个投影是不同的.(2)a在b方向上的投影也可以写成a·b|b|,投影是一个数量,可正可负也可为0,它的符号取决于θ角的范围.返回返回3.向量数量积的性质设a,b是两个非零向量,e是单位向量,α是a与e的夹角,于是我们就有下列数量积的性质:(1)e·a=a·e=|a||e|cosα=|a|cosα.(2)a⊥b⇔a·b=0.(3)a,b同向⇔a·b=|a||b|;a,b反向⇔a·b=-|a||b|.特别地a·a=|a|2=a2或|a|=a·a.(4)若θ为a,b的夹角,则cosθ=a·b|a||b|.(5)|a·b|≤|a|·|b|.返回返回[谨记常用结论](a±b)2=|a±b|2=|a|2±2a·b+|b|2=a2±2a·b+b2;a2-b2=(a+b)(a-b).以上结论可作为公式使用.返回返回4.平面向量数量积的运算律(1)a·b=_____(交换律).(2)λa·b=_______=______(结合律).(3)(a+b)·c=_________(分配律).b·aλ(a·b)a·λ(b)a·c+b·c返回返回[提醒]对于实数a,b,c有(a·b)·c=a·(b·c),但对于向量a,b,c而言,(a·b)·c=a·(b·c)不一定成立,即不满足向量结合律.这是因为(a·b)·c表示一个与c共线的向量,而a·(b·c)表示一个与a共线的向量,而a与c不一定共线,所以(a·...