第五章第二节　平面向量基本定理及坐标表示.pptVIP免费

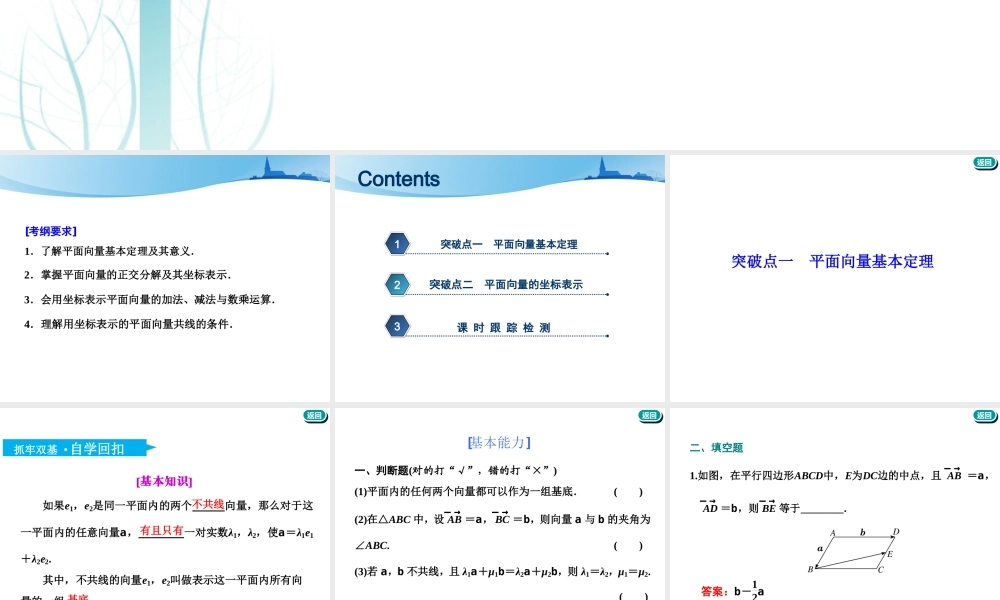
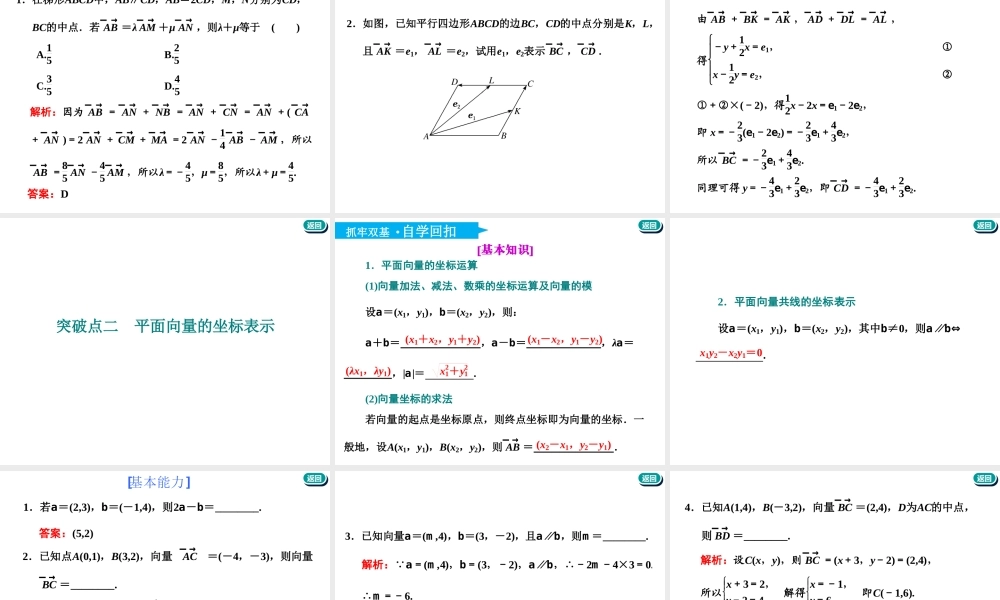
第二节平面向量基本定理及坐标表示[考纲要求]1．了解平面向量基本定理及其意义．2．掌握平面向量的正交分解及其坐标表示．3．会用坐标表示平面向量的加法、减法与数乘运算．4．理解用坐标表示的平面向量共线的条件．突破点一平面向量基本定理1突破点二平面向量的坐标表示2课时跟踪检测3Contents返回返回突破点一平面向量基本定理返回返回抓牢双基·自学回扣[基本知识]如果e1，e2是同一平面内的两个向量，那么对于这一平面内的任意向量a，一对实数λ1，λ2，使a＝λ1e1＋λ2e2.其中，不共线的向量e1，e2叫做表示这一平面内所有向量的一组．不共线有且只有基底返回返回[基本能力]一、判断题(对的打“√”，错的打“×”)(1)平面内的任何两个向量都可以作为一组基底．()(2)在△ABC中，设AB―→＝a，BC―→＝b，则向量a与b的夹角为∠ABC.()(3)若a，b不共线，且λ1a＋μ1b＝λ2a＋μ2b，则λ1＝λ2，μ1＝μ2.()答案：(1)×(2)×(3)√返回返回二、填空题1.如图，在平行四边形ABCD中，E为DC边的中点，且AB―→＝a，AD―→＝b，则BE―→等于________．答案：b－12a返回返回2．设e1，e2是平面内一组基底，若λ1e1＋λ2e2＝0，则λ1＋λ2＝________.答案：03．设e1，e2是平面内一组基底，且a＝e1＋2e2，b＝－e1＋e2，则2a－b＝________.答案：3e1＋3e2返回返回研透高考·深化提能[典例感悟]1.(2019·郑州模拟)如图，在直角梯形ABCD中，AB＝2AD＝2DC，E为BC边上一点，BC―→＝3EC―→，F为AE的中点，则BF―→＝()A．23AB―→－13AD―→B．13AB―→－23AD―→C．－23AB―→＋13AD―→D．－13AB―→＋23AD―→返回返回解析：如图，取AB的中点G，连接DG，CG，易知四边形DCBG为平行四边形，所以BC―→＝GD―→＝AD―→－AG―→＝AD―→－12AB―→，∴AE―→＝AB―→＋BE―→＝AB―→＋23BC―→＝AB―→＋23AD―→－12AB―→＝23AB―→＋23AD―→，于是BF―→＝AF―→－AB―→＝12AE―→－AB―→＝1223AB―→＋23AD―→－AB―→＝－23AB―→＋13AD―→，故选C.答案：C返回返回2．在△ABC中，点P是AB上一点，且CP―→＝23CA―→＋13CB―→，Q是BC的中点，AQ与CP的交点为M，又CM―→＝tCP―→，则实数t的值为________．解析：因为CP―→＝23CA―→＋13CB―→，所以3CP―→＝2CA―→＋CB―→，即2CP―→－2CA―→＝CB―→－CP―→，所以2AP―→＝PB―→.即P为AB的一个三等分点(靠近A点)，返回返回又因为A，M，Q三点共线，设AM―→＝λAQ―→....