第四章第三节　三角函数的图象与性质.pptVIP免费

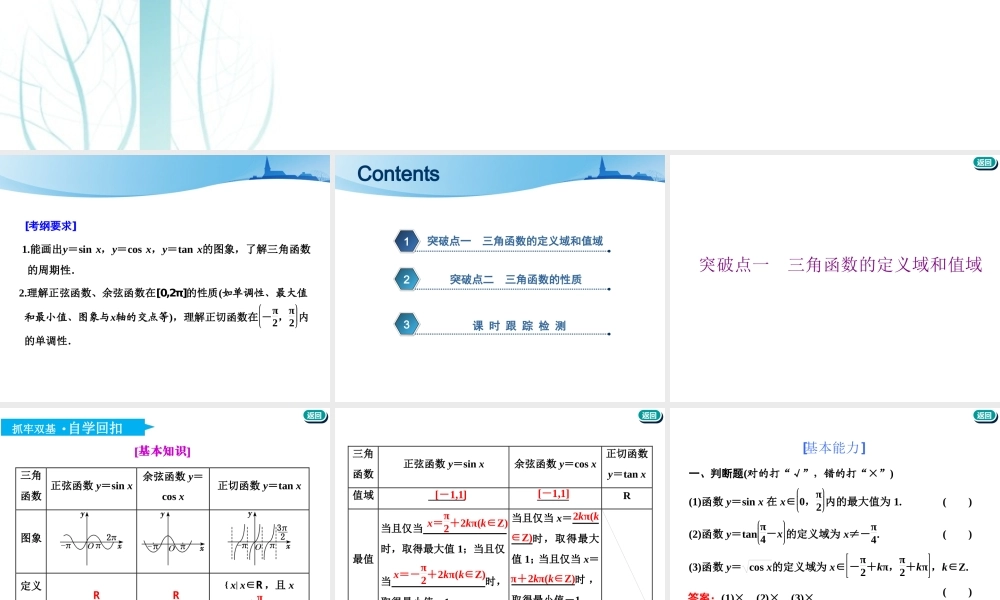
第三节三角函数的图象与性质[考纲要求]1.能画出y＝sinx，y＝cosx，y＝tanx的图象，了解三角函数的周期性．2.理解正弦函数、余弦函数在[0,2π]的性质(如单调性、最大值和最小值、图象与x轴的交点等)，理解正切函数在－π2，π2内的单调性．123Contents突破点一三角函数的定义域和值域突破点二三角函数的性质课时跟踪检测返回返回突破点一三角函数的定义域和值域返回返回抓牢双基·自学回扣[基本知识]三角函数正弦函数y＝sinx余弦函数y＝cosx正切函数y＝tanx图象定义域{x|x∈R，且x≠，k∈ZRRkπ＋π2返回返回三角函数正弦函数y＝sinx余弦函数y＝cosx正切函数y＝tanx值域_____________R最值当且仅当时，取得最大值1；当且仅当时，取得最小值－1当且仅当x＝时，取得最大值1；当且仅当x＝时，取得最小值－1[－1,1][－1,1]x＝π2＋2kπ(k∈Z)x＝－π2＋2kπ(k∈Z)2kπ(k∈Z)π＋2kπ(k∈Z)返回返回[基本能力]一、判断题(对的打“√”，错的打“×”)(1)函数y＝sinx在x∈0，π2内的最大值为1.()(2)函数y＝tanπ4－x的定义域为x≠－π4.()(3)函数y＝cosx的定义域为x∈－π2＋kπ，π2＋kπ，k∈Z.()答案：(1)×(2)×(3)×返回返回二、填空题1．y＝2sinx－2的定义域为________________________．解析：要使函数式有意义，需2sinx－2≥0，即sinx≥22，借助正弦函数的图象(图略)，可得π4＋2kπ≤x≤3π4＋2kπ，k∈Z，所以该函数的定义域是π4＋2kπ，3π4＋2kπ(k∈Z)．答案：π4＋2kπ，3π4＋2kπ(k∈Z)返回返回2．函数y＝2cos2x＋π3，x∈－π6，π6的值域为________．解析： －π6