第三章第一节　导数的概念及运算、定积分.pptVIP免费

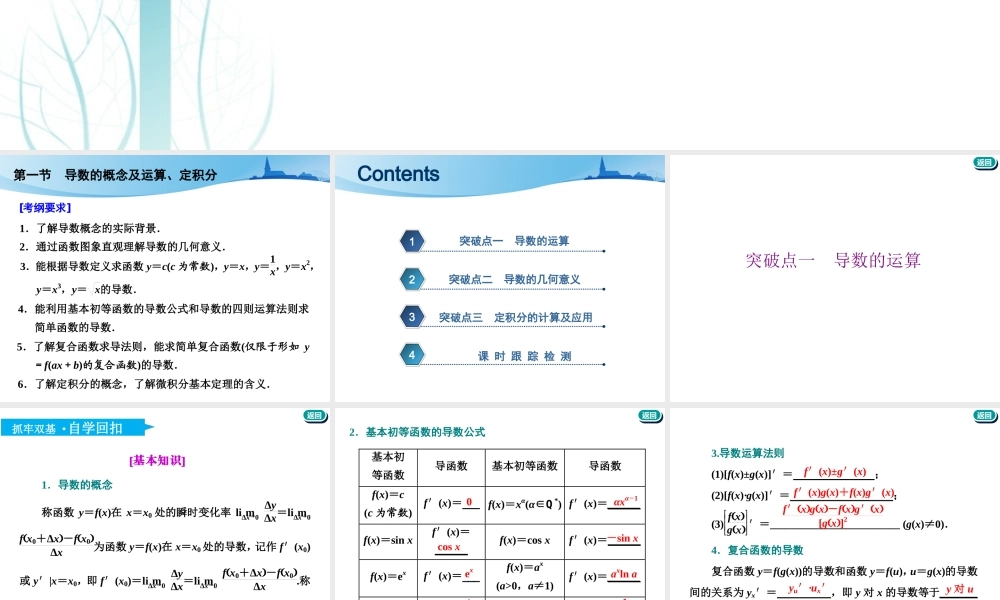
第三章导数及其应用[考纲要求]第一节导数的概念及运算、定积分1．了解导数概念的实际背景．2．通过函数图象直观理解导数的几何意义．3．能根据导数定义求函数y＝c(c为常数)，y＝x，y＝1x，y＝x2，y＝x3，y＝x的导数．4．能利用基本初等函数的导数公式和导数的四则运算法则求简单函数的导数．5．了解复合函数求导法则，能求简单复合函数(仅限于形如y＝f(ax＋b)的复合函数)的导数．6．了解定积分的概念，了解微积分基本定理的含义．1234Contents突破点一导数的运算突破点二导数的几何意义突破点三定积分的计算及应用课时跟踪检测返回返回突破点一导数的运算返回返回抓牢双基·自学回扣[基本知识]1．导数的概念称函数y＝f(x)在x＝x0处的瞬时变化率limΔx→0ΔyΔx＝limΔx→0fx0＋Δx－fx0Δx为函数y＝f(x)在x＝x0处的导数，记作f′(x0)或y′|x＝x0，即f′(x0)＝limΔx→0ΔyΔx＝limΔx→0fx0＋Δx－fx0Δx.称函数f′(x)＝____________________为f(x)的导函数．limΔx→0fx＋Δx－fxΔx返回返回2．基本初等函数的导数公式基本初等函数导函数基本初等函数导函数f(x)＝c(c为常数)f′(x)＝___f(x)＝xα(α∈Q*)f′(x)＝______f(x)＝sinxf′(x)＝______f(x)＝cosxf′(x)＝______f(x)＝exf′(x)＝___f(x)＝ax(a>0，a≠1)f′(x)＝______f(x)＝lnxf′(x)＝___f(x)＝logax(a>0，a≠1)f′(x)＝______0αxα－1cosx－sinxexaxlna1x1xlna返回返回3.导数运算法则(1)[f(x)±g(x)]′＝；(2)[f(x)·g(x)]′＝；(3)fxgx′＝________________________(g(x)≠0)．4．复合函数的导数复合函数y＝f(g(x))的导数和函数y＝f(u)，u＝g(x)的导数间的关系为yx′＝，即y对x的导数等于_______的导数与的导数的乘积．f′(x)±g′(x)f′(x)g(x)＋f(x)g′(x)f′xgx－fxg′x[gx]2yu′·ux′y对uu对x返回返回[基本能力]一、判断题(对的打“√”，错的打“×”)(1)f′(x0)与(f(x0))′的计算结果相同．()(2)求f′(x0)时，可先求f(x0)再求f′(x0)．()(3)f′(x0)是导函数f′(x)在x＝x0处的函数值．()答案：(1)×(2)×(3)√返回返回二、填空题1．函数y＝xcosx－sinx的导数为________．解析： f′(x)＝－8＋4x，∴f′(x0)＝－8＋4x0＝4，解得x0＝3.2．已知f(x)＝13－8x＋2x2，f′(x0)＝4，则x0＝________.答案：－xsinx答案：3返回返回3．已知函数f(x)＝f′π4cosx＋sinx，则fπ4的值为______...