第三章第二节　第3课时　题型研究——“函数与导数”大题常考的3类题型.pptVIP免费

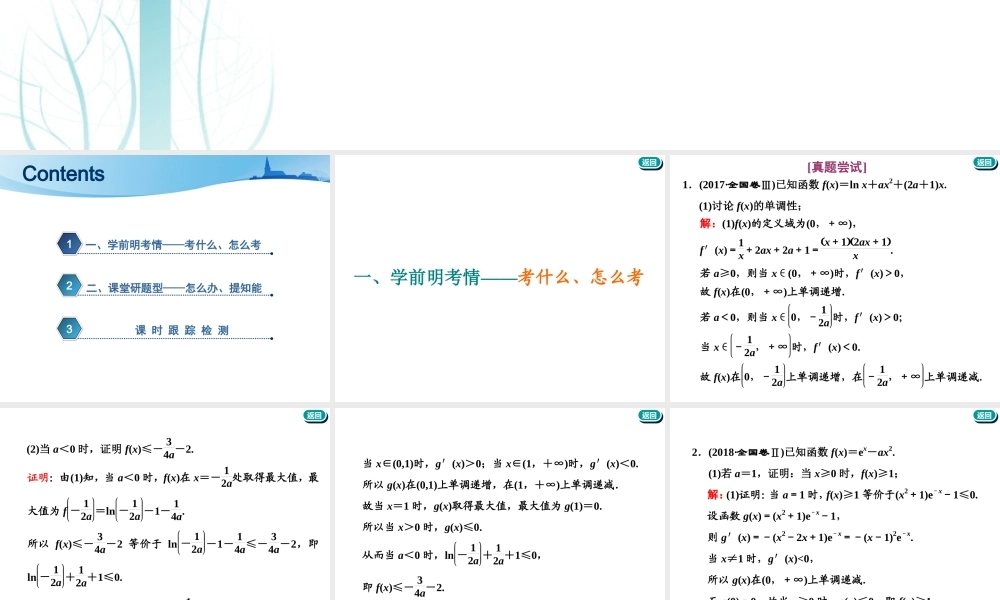
第3课时题型研究——“函数与导数”大题常考的3类题型123Contents一、学前明考情——考什么、怎么考二、课堂研题型——怎么办、提知能课时跟踪检测返回返回一、学前明考情——考什么、怎么考返回返回[真题尝试]1．(2017·全国卷Ⅲ)已知函数f(x)＝lnx＋ax2＋(2a＋1)x.(1)讨论f(x)的单调性；解：(1)f(x)的定义域为(0，＋∞)，f′(x)＝1x＋2ax＋2a＋1＝x＋12ax＋1x.若a≥0，则当x∈(0，＋∞)时，f′(x)＞0，故f(x)在(0，＋∞)上单调递增．若a＜0，则当x∈0，－12a时，f′(x)＞0；当x∈－12a，＋∞时，f′(x)＜0.故f(x)在0，－12a上单调递增，在－12a，＋∞上单调递减．返回返回(2)当a＜0时，证明f(x)≤－34a－2.证明：由(1)知，当a＜0时，f(x)在x＝－12a处取得最大值，最大值为f－12a＝ln－12a－1－14a.所以f(x)≤－34a－2等价于ln－12a－1－14a≤－34a－2，即ln－12a＋12a＋1≤0.设g(x)＝lnx－x＋1，则g′(x)＝1x－1.返回返回当x∈(0,1)时，g′(x)＞0；当x∈(1，＋∞)时，g′(x)＜0.所以g(x)在(0,1)上单调递增，在(1，＋∞)上单调递减．故当x＝1时，g(x)取得最大值，最大值为g(1)＝0.所以当x＞0时，g(x)≤0.从而当a＜0时，ln－12a＋12a＋1≤0，即f(x)≤－34a－2.返回返回2．(2018·全国卷Ⅱ)已知函数f(x)＝ex－ax2.(1)若a＝1，证明：当x≥0时，f(x)≥1；解：(1)证明：当a＝1时，f(x)≥1等价于(x2＋1)e－x－1≤0.设函数g(x)＝(x2＋1)e－x－1，则g′(x)＝－(x2－2x＋1)e－x＝－(x－1)2e－x.当x≠1时，g′(x)<0，所以g(x)在(0，＋∞)上单调递减．而g(0)＝0，故当x≥0时，g(x)≤0，即f(x)≥1.返回返回(2)若f(x)在(0，＋∞)只有一个零点，求a.解：设函数h(x)＝1－ax2e－x.f(x)在(0，＋∞)上只有一个零点等价于h(x)在(0，＋∞)上只有一个零点．(ⅰ)当a≤0时，h(x)>0，h(x)没有零点；(ⅱ)当a>0时，h′(x)＝ax(x－2)e－x.当x∈(0,2)时，h′(x)<0；当x∈(2，＋∞)时，h′(x)>0.所以h(x)在(0,2)上单调递减，在(2，＋∞)上单调递增．故h(2)＝1－4ae2是h(x)在(0，＋∞)上的最小值．返回返回①当h(2)>0，即ae24时，因为h(0)＝1，所以h(x)在(0,2)上有一个零点．由(1)知，当x>0时，ex>x2，所以h(4a)＝1－16a3e4a＝1－16a3e2a...