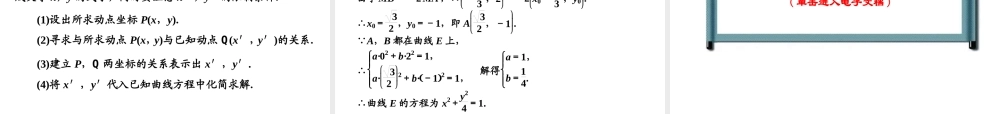第九章第六节 曲线与方程.pptVIP免费

第六节曲线与方程[考纲要求]1.了解曲线与方程的对应关系．2.能够根据所给条件选择恰当的方法(直接法、定义法、代入法)求曲线的轨迹方程．抓牢双基·自学回扣1研透高考·深化提能2课时跟踪检测3Contents返回返回抓牢双基·自学回扣[基本知识]1．曲线与方程一般地，在平面直角坐标系中，如果某曲线C上的点与一个二元方程f(x，y)＝0的实数解建立了如下关系：(1)曲线上点的坐标都是．(2)以这个方程的解为坐标的点都是．那么这个方程叫做曲线的方程，这条曲线叫做．这个方程的解曲线上的点方程的曲线返回返回2．求动点轨迹方程的一般步骤(1)建立适当的坐标系，用有序实数对(x，y)表示曲线上任意一点M的坐标．(2)写出适合条件p的点M的集合P＝{M|p(M)}．(3)用坐标表示条件p(M)，列出方程.(4)化方程f(x，y)＝0为最简形式．(5)说明以化简后的方程的解为坐标的点都在曲线上．f(x，y)＝0返回返回3．曲线的交点设曲线C1的方程为F1(x，y)＝0，曲线C2的方程为F2(x，y)＝0，则C1，C2的交点坐标即为方程组的实数解．若此方程组，则两曲线无交点．F1x，y＝0，F2x，y＝0无解返回返回[基本能力]一、判断题(对的打“√”，错的打“×”)(1)过点P(x0，y0)斜率为k的直线的方程是y－y0x－y0＝k.()(2)若点P(x0，y0)在曲线C上，则有f(x0，y0)＝0.()答案：(1)×(2)√返回返回二、填空题1．方程x2＋2y2－4x＋8y＋12＝0表示的图形为________．答案：一个点(2，－2)2．已知两点M(－2,0)，N(2,0)，点P满足PM―→·PN―→＝12，则点P的轨迹方程为________．答案：x2＋y2＝16返回返回研透高考·深化提能方法一直接法求轨迹方程[例1](1)(2019·葫芦岛调研)在△ABC中，已知A(2,0)，B(－2，0)，G，M为平面上的两点且满足GA―→＋GB―→＋GC―→＝0，|MA―→|＝|MB―→|＝|MC―→|，GM―→∥AB―→，则顶点C的轨迹为()A．焦点在x轴上的椭圆(长轴端点除外)B．焦点在y轴上的椭圆(短轴端点除外)C．焦点在x轴上的双曲线(实轴端点除外)D．焦点在x轴上的抛物线(顶点除外)[解析]设C(x，y)(y≠0)，则由GA―→＋GB―→＋GC―→＝0，即G为△ABC的重心，得Gx3，y3.又|MA―→|＝|MB―→|＝|MC―→|，即M为△ABC的外心，所以点M在y轴上，又GM―→∥AB―→，则有M0，y3.所以x2＋y－y32＝4＋y29，化简得x24＋y212＝1，y≠0.所以顶点C的轨迹为焦点在y轴上的椭圆(除去短轴端点)．[答案]B返回返回(2)已知△ABC的顶点B(0,0)，C(5,0)，AB边上的中线长...