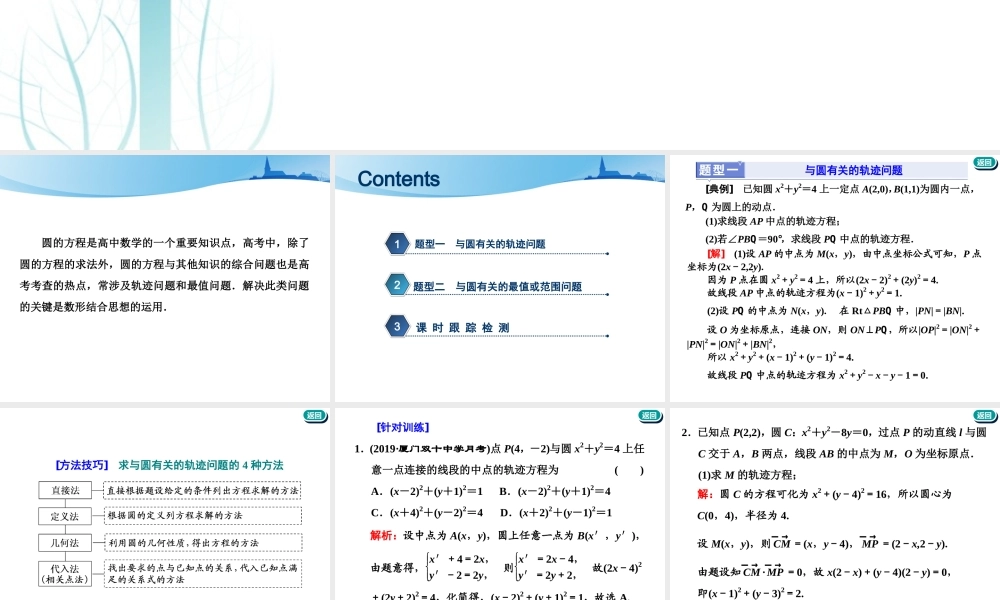
第3课时深化提能——与圆有关的综合问题圆的方程是高中数学的一个重要知识点,高考中,除了圆的方程的求法外,圆的方程与其他知识的综合问题也是高考考查的热点,常涉及轨迹问题和最值问题.解决此类问题的关键是数形结合思想的运用.题型一与圆有关的轨迹问题1题型二与圆有关的最值或范围问题2课时跟踪检测3Contents返回返回与圆有关的轨迹问题[典例]已知圆x2+y2=4上一定点A(2,0),B(1,1)为圆内一点,P,Q为圆上的动点.(1)求线段AP中点的轨迹方程;(2)若∠PBQ=90°,求线段PQ中点的轨迹方程.[解](1)设AP的中点为M(x,y),由中点坐标公式可知,P点坐标为(2x-2,2y).因为P点在圆x2+y2=4上,所以(2x-2)2+(2y)2=4.故线段AP中点的轨迹方程为(x-1)2+y2=1.(2)设PQ的中点为N(x,y).在Rt△PBQ中,|PN|=|BN|.设O为坐标原点,连接ON,则ON⊥PQ,所以|OP|2=|ON|2+|PN|2=|ON|2+|BN|2,所以x2+y2+(x-1)2+(y-1)2=4.故线段PQ中点的轨迹方程为x2+y2-x-y-1=0.返回返回[方法技巧]求与圆有关的轨迹问题的4种方法返回返回[针对训练]1.(2019·厦门双十中学月考)点P(4,-2)与圆x2+y2=4上任意一点连接的线段的中点的轨迹方程为()A.(x-2)2+(y+1)2=1B.(x-2)2+(y+1)2=4C.(x+4)2+(y-2)2=4D.(x+2)2+(y-1)2=1解析:设中点为A(x,y),圆上任意一点为B(x′,y′),由题意得,x′+4=2x,y′-2=2y,则x′=2x-4,y′=2y+2,故(2x-4)2+(2y+2)2=4,化简得,(x-2)2+(y+1)2=1,故选A.答案:A返回返回2.已知点P(2,2),圆C:x2+y2-8y=0,过点P的动直线l与圆C交于A,B两点,线段AB的中点为M,O为坐标原点.(1)求M的轨迹方程;解:圆C的方程可化为x2+(y-4)2=16,所以圆心为C(0,4),半径为4.设M(x,y),则CM―→=(x,y-4),MP―→=(2-x,2-y).由题设知CM―→·MP―→=0,故x(2-x)+(y-4)(2-y)=0,即(x-1)2+(y-3)2=2.由于点P在圆C的内部,所以M的轨迹方程是(x-1)2+(y-3)2=2.返回返回(2)当|OP|=|OM|时,求l的方程及△POM的面积.解:由(1)可知M的轨迹是以点N(1,3)为圆心,2为半径的圆.由于|OP|=|OM|,故O在线段PM的垂直平分线上.又P在圆N上,从而ON⊥PM.因为ON的斜率为3,所以l的斜率为-13,故l的方程为x+3y-8=0.又|OM|=|OP|=22,O到l的距离为4105,所以|PM|=4105,S△POM=12×4105×4105=165,故△POM的面积为165.返回返回与圆有关的最值或范围问题[例1](2...