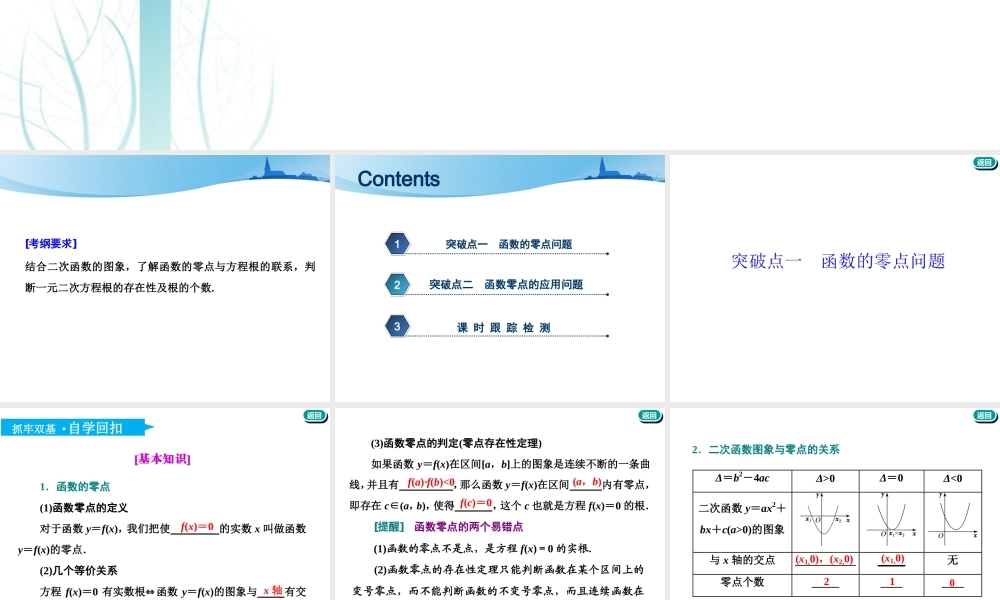
第七节函数与方程[考纲要求]结合二次函数的图象,了解函数的零点与方程根的联系,判断一元二次方程根的存在性及根的个数.突破点一函数的零点问题1突破点二函数零点的应用问题2课时跟踪检测3Contents返回返回突破点一函数的零点问题返回返回抓牢双基·自学回扣[基本知识]1.函数的零点(1)函数零点的定义对于函数y=f(x),我们把使的实数x叫做函数y=f(x)的零点.(2)几个等价关系方程f(x)=0有实数根⇔函数y=f(x)的图象与有交点⇔函数y=f(x)有.f(x)=0x轴零点返回返回(3)函数零点的判定(零点存在性定理)如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有,那么函数y=f(x)在区间内有零点,即存在c∈(a,b),使得,这个c也就是方程f(x)=0的根.[提醒]函数零点的两个易错点f(a)·f(b)<0(a,b)f(c)=0(1)函数的零点不是点,是方程f(x)=0的实根.(2)函数零点的存在性定理只能判断函数在某个区间上的变号零点,而不能判断函数的不变号零点,而且连续函数在一个区间的端点处函数值异号是这个函数在这个区间上存在零点的充分不必要条件.返回返回2.二次函数图象与零点的关系Δ=b2-4acΔ>0Δ=0Δ<0二次函数y=ax2+bx+c(a>0)的图象与x轴的交点________________无零点个数_____________(x1,0),(x2,0)(x1,0)210返回返回[基本能力]一、判断题(对的打“√”,错的打“×”)(1)函数的零点就是函数的图象与x轴的交点.()(2)函数y=f(x),x∈D在区间(a,b)⊆D内有零点(函数图象连续不断),则f(a)·f(b)<0.()(3)二次函数y=ax2+bx+c在b2-4ac<0时没有零点.()答案:(1)×(2)×(3)√返回返回二、填空题1.若函数f(x)=ax-b有一个零点是3,那么函数g(x)=bx2+3ax的零点是________.解析: 函数f(x)=ax-b的零点是3,∴3a-b=0,即b=3a.于是函数g(x)=bx2+3ax=bx2+bx=bx(x+1),令g(x)=0,得x=0或x=-1.答案:0,-1返回返回2.函数f(x)=ex+12x-2的零点个数为________.解析: f′(x)=ex+12>0,∴f(x)在R上单调递增,又f(0)=1-2<0,f(1)=e-32>0,∴函数f(x)在定义域内有零点且只有一个.答案:1返回返回3.若函数f(x)=ax+1-2a在区间(-1,1)上存在一个零点,则实数a的取值范围是________.解析:当a=0时,函数f(x)=1在(-1,1)上没有零点,所以a≠0.所以函数f(x)是单调函数,要满足题意,只需f(-1)f(1)<0,即(-3a+1)·(1-a)<0,所以(a-1)·(3a-1)<0,解得13