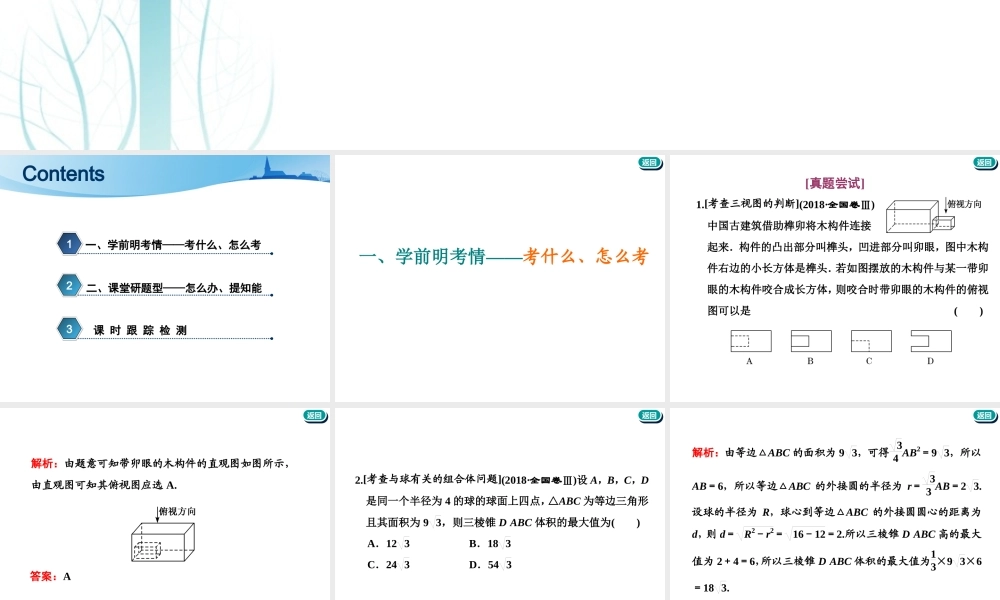
第2课时系统题型——空间几何体的表面积、体积123Contents一、学前明考情——考什么、怎么考二、课堂研题型——怎么办、提知能课时跟踪检测返回返回一、学前明考情——考什么、怎么考返回返回[真题尝试]1.[考查三视图的判断](2018·全国卷Ⅲ)中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是()返回返回解析:由题意可知带卯眼的木构件的直观图如图所示,由直观图可知其俯视图应选A.答案:A返回返回2.[考查与球有关的组合体问题](2018·全国卷Ⅲ)设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为93,则三棱锥DABC体积的最大值为()A.123B.183C.243D.543返回返回解析:由等边△ABC的面积为93,可得34AB2=93,所以AB=6,所以等边△ABC的外接圆的半径为r=33AB=23.设球的半径为R,球心到等边△ABC的外接圆圆心的距离为d,则d=R2-r2=16-12=2.所以三棱锥DABC高的最大值为2+4=6,所以三棱锥DABC体积的最大值为13×93×6=183.答案:B返回返回3.[考查圆锥的侧面积求法](2018·全国卷Ⅱ)已知圆锥的顶点为S,母线SA,SB所成角的余弦值为78,SA与圆锥底面所成角为45°,若△SAB的面积为515,则该圆锥的侧面积为________.解析:如图, SA与底面成45°角,∴△SAO为等腰直角三角形.设OA=r,则SO=r,SA=SB=2r.在△SAB中,cos∠ASB=78,∴sin∠ASB=158,∴S△SAB=12SA·SB·sin∠ASB=12×(2r)2×158=515,解得r=210,∴SA=2r=45,即母线长l=45,∴S圆锥侧=πrl=π×210×45=402π.答案:402π返回返回[把握考情]创新角度常规角度常将球与多面体、旋转体结合,涉及最值问题交汇考查,也常与数学文化结合1.几何体的三视图.重点考查由几何体三视图识别几何体.2.求几何体的体积.重点考查规则几何体与组合体的体积的求解及由三视图得到的几何体的体积的求解.3.求几何体的表面积.重点考查组合体的表面积的求解.以选择题或填空题的形式考查,属于中档题目返回返回二、课堂研题型——怎么办、提知能返回返回空间几何体的三视图[典例感悟]1.(2018·贵州黔东南州一模)若某几何体的三视图如图所示,则这个几何体的直观图可以是()返回返回解析:选项A的正视图、俯视图不符合要求,选项B的正视图、侧视图不符合要求,选项C的俯视图不符合要求,通过...