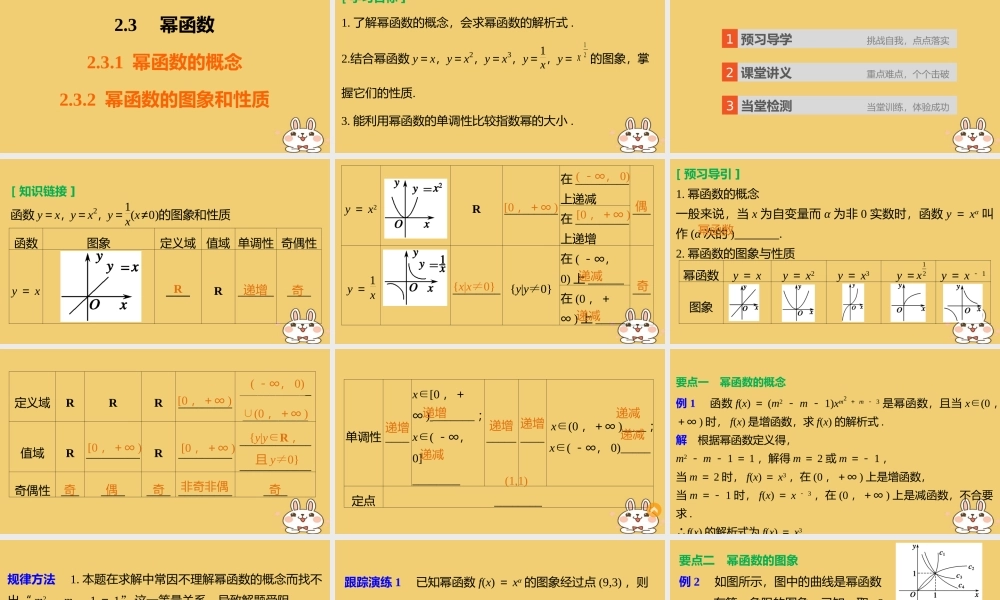
第2章——指数函数、对数函数指数函数、对数函数和幂函数和幂函数2.3幂函数2.3.1幂函数的概念2.3.2幂函数的图象和性质[学习目标]1.了解幂函数的概念,会求幂函数的解析式.2.结合幂函数y=x,y=x2,y=x3,y=1x,y=12x的图象,掌握它们的性质.3.能利用幂函数的单调性比较指数幂的大小.1预习导学挑战自我,点点落实2课堂讲义重点难点,个个击破3当堂检测当堂训练,体验成功[知识链接]函数y=x,y=x2,y=1x(x≠0)的图象和性质函数图象定义域值域单调性奇偶性y=x____R__________R递增奇y=x2R_________在_________上递减___在_________上递增y=________{y|y≠0}在(-∞,0)上_________在(0,+∞)上_____[0,+∞)(-∞,0)[0,+∞){x|x≠0}递减递减偶奇1x[预习导引]1.幂函数的概念一般来说,当x为自变量而α为非0实数时,函数y=xα叫作(α次的).2.幂函数的图象与性质幂函数y=xy=x2y=x3y=y=x-1图象12x幂函数定义域RRR_______________________________值域R_________R_________________________________奇偶性________________________[0,+∞)(-∞,0)∪(0,+∞)[0,+∞)[0,+∞){y|y∈R,且y≠0}奇偶奇非奇非偶奇单调性____x∈[0,+∞)_______;x∈(-∞,0]_________________x∈(0,+∞)____;x∈(-∞,0)_____定点________递增递增递减递增递增递减递减(1,1)要点一幂函数的概念例1函数f(x)=(m2-m-1)xm2+m-3是幂函数,且当x∈(0,+∞)时,f(x)是增函数,求f(x)的解析式.解根据幂函数定义得,m2-m-1=1,解得m=2或m=-1,当m=2时,f(x)=x3,在(0,+∞)上是增函数,当m=-1时,f(x)=x-3,在(0,+∞)上是减函数,不合要求.∴f(x)的解析式为f(x)=x3规律方法1.本题在求解中常因不理解幂函数的概念而找不出“m2-m-1=1”这一等量关系,导致解题受阻.2.幂函数y=xα(α∈R)中,α为常数,系数为1,底数为单一的x.这是判断一个函数是否为幂函数的重要依据和唯一标准.幂函数与指数函数的解析式形同而实异,解题时一定要分清,以防出错.跟踪演练1已知幂函数f(x)=xα的图象经过点(9,3),则f(100)=________.解析由题意可知f(9)=3,即9α=3,∴α=12,∴f(x)=12x,∴f(100)=12100=10.10要点二幂函数的图象例2如图所示,图中的曲线是幂函数y=xn在第一象限的图象,已知n取±2,±四个值,则相应于c1,c2,c3,c4的n依次为()12A.-2,-12,12,2B.2,12,-12,-2C.-12,-2,2,12D.2,12,-2,-12解析考虑...