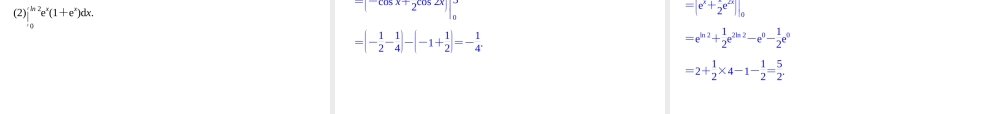2017-2018学年湘教版数学选修2-2配套课件：4-5-4微积分基本定理 -数学备课大师【全免费】.pptVIP免费

高中数学·选修2-2·湘教版4．5.4微积分基本定理[[学习目标学习目标]]了了解导数与定积分的关系，了解微积分基本解导数与定积分的关系，了解微积分基本定理，并能正确运用基本定理计算简单的定定理，并能正确运用基本定理计算简单的定积分．积分．[[知识链接知识链接]]11．．导导数与定积分有怎样的联系？数与定积分有怎样的联系？答答导导数与定积分都是定积分学中两个最数与定积分都是定积分学中两个最基本、最重要的概念，运用它们之间的联基本、最重要的概念，运用它们之间的联系，我们可以找出求定积分的方法，求导系，我们可以找出求定积分的方法，求导数与定积分是互为逆运算．数与定积分是互为逆运算．22．在下面图．在下面图(1)(1)、图、图(2)(2)、图、图(3)(3)中的三个中的三个图形阴影部分的面积分别怎样表示？图形阴影部分的面积分别怎样表示？答根据定积分与曲边梯形的面积的关系知：图(1)中S＝abf(x)dx，图(2)中S＝－abf(x)dx，图(3)中S＝0bf(x)dx－a0f(x)dx.[预习导引]1．微积分基本定理如果f(x)是在[a，b]上有定义的连续函数，F(x)在[a，b]上可导并且F′(x)＝f(x)，则abf(t)dt＝．F(b)－F(a)2．微积分基本定理的直观理解画出[a，b]上的函数y＝F(x)的曲线，设f(x)是F(x)的导数，取分点：a＝x0＜x1＜x2＜…＜xn－1＜xn＝b.记xk－1－xk＝Δxk，显然有F(b)－F(a)＝∑n－1k＝0(F(xk－1)－F(xk))＝∑n－1k＝0(Fxk－1－Fxkxk－1－xk)Δxk，左端和式里的分式Fxk－1－Fxkxk－1－xk就是图中对应的小直角三角形的斜边的．分点越密，这斜率越接近于曲线在点(xk，F(xk))处的的斜率，也就是F(x)在xk处的．所以这和式越来越接近和式∑n－1k＝0f(xk)Δxk.而当分点无限加密时，最后的这个和式就成了f(x)在[a，b]上的．斜率切线导数F′(xk)定积分要点一求简单函数的定积分例1计算下列定积分：(1)123dx；(2)02(2x＋3)dx；(3)(4x－x2)dx；(4)12(x－1)5dx.解(1)因为(3x)′＝3，所以123dx＝(3x)21＝3×2－3×1＝3.(2)因为(x2＋3x)′＝2x＋3，所以02(2x＋3)dx＝(x2＋3x)20＝22＋3×2－(02＋3×0)＝10.(3)因为2x2－x33′＝4x－x2，所以(4x－x2)dx＝2x2－x333－1＝2×32－333－2×－12－－133＝203.(4)因为16x－16′＝(x－1)5，所以21(x－1)5d...