高二【数学（人教B版）】7空间中的点、直线与空间向量（1）-课件.pptxVIP免费

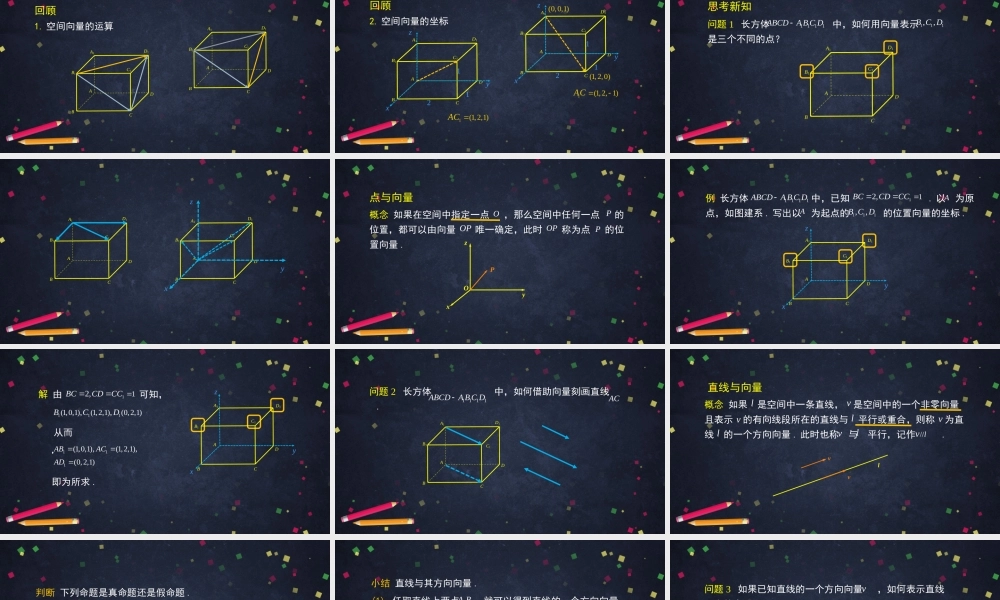
空间中的点、直线与空间向量（1）高二年级数学主讲人：叶彩娟北京市第四中学北京市中小学空中课堂回顾1.空间向量的运算DCBAD1C1B1A1DCBAD1C1B1A1回顾2.空间向量的坐标DCBAD1C1B1A1xyz112DCBAD1C1B1A1xyz112(1,2,0)(0,0,1)1(1,2,1)AC�1(1,2,1)AC�问题1长方体中，如何用向量表示是三个不同的点？1111ABCDABCD111,,BCDDCBAD1C1B1A1思考新知DCBAD1C1B1A1DCBAD1C1B1A1xyz概念如果在空间中指定一点，那么空间中任何一点的位置，都可以由向量唯一确定，此时称为点的位置向量.OP�POOP�PPOzyx点与向量例长方体中，已知.以为原点，如图建系.写出以为起点的的位置向量的坐标.1111ABCDABCD112,BCCDCCA111,,BCDxyzDCBAD1C1B1A1A解由可知，112,BCCDCC111(1,0,1)(1,2,1)(0,2,1),,BCDxyz从而111(1,0,1)(1,2,1)(0,2,1),,ABACAD��即为所求.DCBAD1C1B1A1DCBAD1C1B1A1问题2长方体中，如何借助向量刻画直线.1111ABCDABCDAC概念如果是空间中一条直线，是空间中的一个非零向量且表示的有向线段所在的直线与平行或重合，则称为直线的一个方向向量.此时也称与平行，记作.lllvvvvl//lvlvv直线与向量判断下列命题是真命题还是假命题.(1)已知是直线上的两个点，则是的一个方向向量.,ABllAB�(2)直线的任意两个方向向量都是同向的.l(3)如果是的一个方向向量，是的一个方向向量，且,则与重合.1v1l2v2l12=vv1l2l小结直线与其方向向量.(2)直线的方向向量不唯一，但是任意两个方向向量都是互相平行的.(3)直线的方向向量相同，平行或者重合.12,ll12,ll(1)任取直线上两点，就可以得到直线的一个方向向量.,ABAB�问题3如果已知直线的一个方向向量，如何表示直线上的点.PPvvA结论已知直线的一个方向向量和直线上一点，对于直线上任意一点，存在唯一的实数，使得.进一步的，设是空间中任意一点，有.lAvPPlAvvvAP�lvOPOA�OvAP�vOPOA�(1)当且仅当.(2)当且仅当.判断设,分别是空间中两条不重合的直线和的方向向量，下列命题是否正确.1v12//ll2v2l1l12//vv12ll12vv例正方体中，分别为棱的中点.求证：（1）；（2）与不平行.1111ABCDABCD,EF1//EFAC1EA1BD11,ABCDFEDCBAD1C1B1A1证明如图建系,以正方体棱长作为单位长度，则111(1,0,1),(1,1,0),(1,,0)21(0,1,0),(0,0,1),(0,,1)2BECFAD从而1111(0,,1),(0,,1),22(1,1,1)ECFABD��FEDCBAD1C1B1A1xyz1111(0,,...