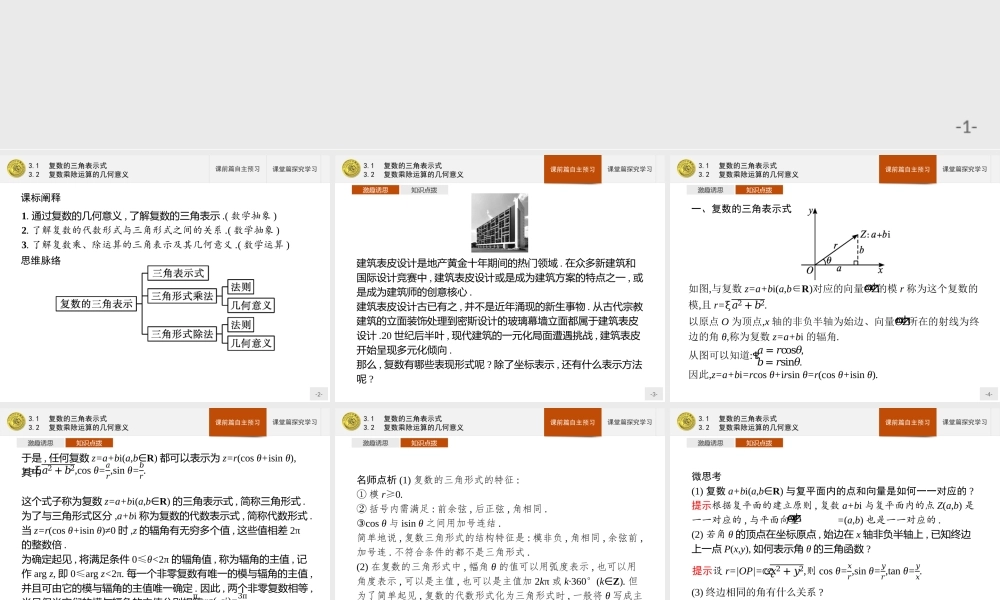
-1-3.1复数的三角表示式3.2复数乘除运算的几何意义-2-3.1复数的三角表示式3.2复数乘除运算的几何意义课前篇自主预习课堂篇探究学习课标阐释1.通过复数的几何意义,了解复数的三角表示.(数学抽象)2.了解复数的代数形式与三角形式之间的关系.(数学抽象)3.了解复数乘、除运算的三角表示及其几何意义.(数学运算)思维脉络-3-3.1复数的三角表示式3.2复数乘除运算的几何意义课前篇自主预习课堂篇探究学习课前篇自主预习激趣诱思知识点拨建筑表皮设计是地产黄金十年期间的热门领域.在众多新建筑和国际设计竞赛中,建筑表皮设计或是成为建筑方案的特点之一,或是成为建筑师的创意核心.建筑表皮设计古已有之,并不是近年涌现的新生事物.从古代宗教建筑的立面装饰处理到密斯设计的玻璃幕墙立面都属于建筑表皮设计.20世纪后半叶,现代建筑的一元化局面遭遇挑战,建筑表皮开始呈现多元化倾向.那么,复数有哪些表现形式呢?除了坐标表示,还有什么表示方法呢?-4-3.1复数的三角表示式3.2复数乘除运算的几何意义课前篇自主预习课堂篇探究学习课前篇自主预习激趣诱思知识点拨一、复数的三角表示式如图,与复数z=a+bi(a,b∈R)对应的向量𝑂𝑍ሬሬሬሬሬԦ的模r称为这个复数的模,且r=ξ𝑎2+𝑏2.以原点O为顶点,x轴的非负半轴为始边、向量𝑂𝑍ሬሬሬሬሬԦ所在的射线为终边的角θ,称为复数z=a+bi的辐角.从图可以知道:ቄ𝑎=𝑟cos𝜃,𝑏=𝑟sin𝜃.因此,z=a+bi=rcosθ+irsinθ=r(cosθ+isinθ).-5-3.1复数的三角表示式3.2复数乘除运算的几何意义课前篇自主预习课堂篇探究学习课前篇自主预习激趣诱思知识点拨于是,任何复数z=a+bi(a,b∈R)都可以表示为z=r(cosθ+isinθ),其中这个式子称为复数z=a+bi(a,b∈R)的三角表示式,简称三角形式.为了与三角形式区分,a+bi称为复数的代数表示式,简称代数形式.当z=r(cosθ+isinθ)≠0时,z的辐角有无穷多个值,这些值相差2π的整数倍.为确定起见,将满足条件0≤θ<2π的辐角值,称为辐角的主值,记作argz,即0≤argz<2π.每一个非零复数有唯一的模与辐角的主值,并且可由它的模与辐角的主值唯一确定.因此,两个非零复数相等,当且仅当它们的模与辐角的主值分别相等.显然当a>0时,arga=0,arg(-a)=π,arg(ai)如果z=0,那么与它对应的向量缩成一个点(零向量),它的方向是任意的,所以复数0的辐角也是任意的.r=ξ𝑎2+𝑏2,cosθ=𝑎𝑟,sinθ=𝑏𝑟.=π2,arg(-ai)=3π2.𝑂𝑍ሬሬሬሬሬԦ-6-3.1复数的三角表示式3.2复数乘除运算的几何意义课前篇自主预习课堂篇探究学习课前篇自...