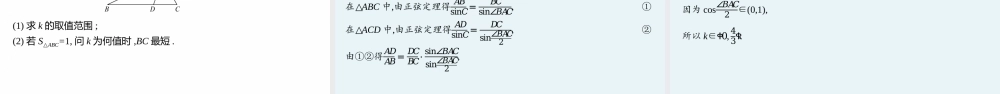高中同步学案优化设计GAOZHONGTONGBUXUEANYOUHUASHEJI第3课时习题课——正弦定理和余弦定理的综合应用第六章2022课堂篇探究学习探究一利用正弦定理、余弦定理解三角形例1在△ABC中,a,b,c分别是角A,B,C所对的边,若bsinA=3csinB,a=3,cosB=23,则b=()A.14B.6C.ξ14D.ξ6分析先由bsinA=3csinB及正弦定理得出边a,c的关系,从而得到边a,c的长度,再利用余弦定理求出b.答案D解析由bsinA=3csinB及正弦定理,得ab=3bc,即a=3c.因为a=3,所以c=1.由余弦定理,得b=ට𝑎2+𝑐2-2𝑎𝑐cos𝐵=ට32+12-2×3×1×23=ξ6.要点笔记正弦定理、余弦定理解三角形的求解策略应用正弦定理、余弦定理解决三角形问题,关键是根据已知条件对边和角进行相互转化,化简表达式,通过代数变形或三角恒等变换解决问题.变式训练1△ABC的内角A,B,C的对边分别为a,b,c,已知csinC-bsinB=2asinA,c=2b,则sinA=()A.ඥ158B.78C.ඥ55D.2ඥ55答案A解析在△ABC中,已知csinC-bsinB=2asinA,整理得c2-b2=2a2,因为c=2b,所以ξ3b=ξ2a,a=ඥ3𝑏ඥ2.故根据余弦定理的推论,得cosA=𝑏2+𝑐2-𝑎22𝑏𝑐=78.因为0