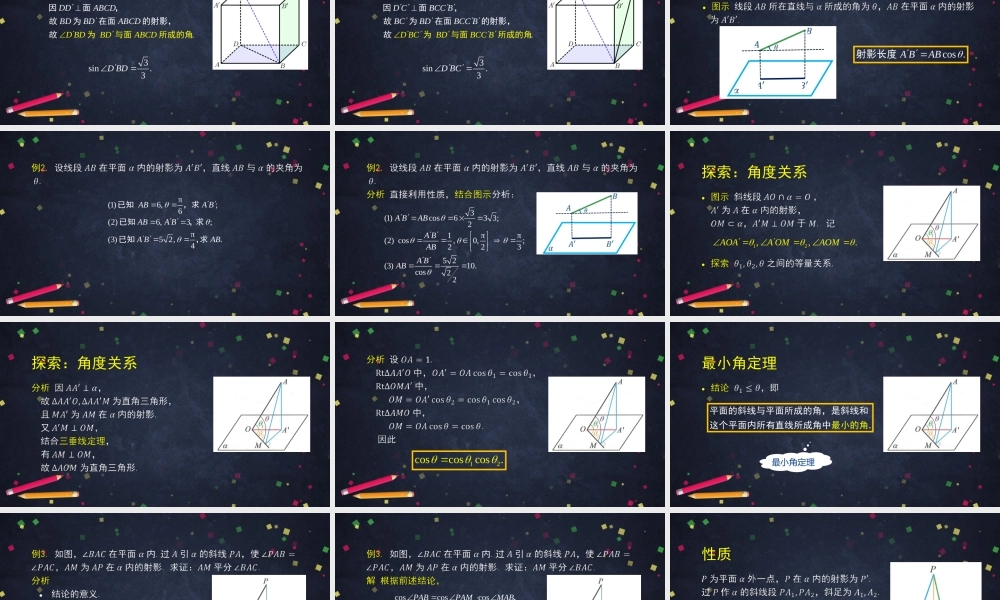
直线与平面的夹角(1)高二年级数学主讲人周康北京市第四中学北京市中小学空中课堂根据直线与平面公共点的个数分为:回忆:直线与平面的位置关系l线在面内:l线面平行:∥l线面相交:问题如何刻画直线与平面所成的角?情境:直线与平面形成角度特殊情形:或ll∥,.lmlm一般情形:斜线与平面所成角斜线与射影定义平面的斜线与它在平面内的射影所成的锐角,称为这条斜线与平面所成的角.斜线与平面所成的角BAABAABBABAB是平面的斜.线,斜足为内是与平,是在面所射影.成的角的注记.DDABCDBDBDBDBDABCADDBCD因射为与面面,故为在面的影,所成的角故3sin.3DBD.DCBCCBBCBDBCCBDBCBDBCCB因面,故为在面的射影,故为与面所成的角3sin.3DBC性质:射影长度cos.ABAB射影长度π(1)6,;6(2)6,3;π(3)52,.4ABABABABABAB已知,求已知,求已知,求3(1)cos633;21ππ(2)cos,0,;22352(3)10.cos22ABABABABABAB探索:角度关系12,,.AOAAOMAOM探索:角度关系12coscoscos.最小角定理平面的斜线与平面所成的角,是斜线和这个平面内所有直线所成角中最小的角.最小角定理coscoscoscoscoscoscoscos..PABPAMMABPACPAMMACPABPACMABMACMABMACAMBAC,,由得故,即平分性质121212.PAPAPAPA总结为:性质斜线段长、射影长、.经斜线与平面的所成的,角,过平面外同一点所作多条斜线中三者其一相等,另两个也相等基本想法:利用线线角刻画线面角.基本思路:1.找/作射影——依靠垂直关系.2.定/求夹角——平面角.性质/结论:结合图示,把握斜线、射影、线面角之间的关系.小结:直线与平面所成的角教材第46页练习A1,2.作业教材第46页练习B2.作业谢谢