0916高二【数学（人教B版）12】直线与平面的夹角（2）-课件.pptxVIP免费

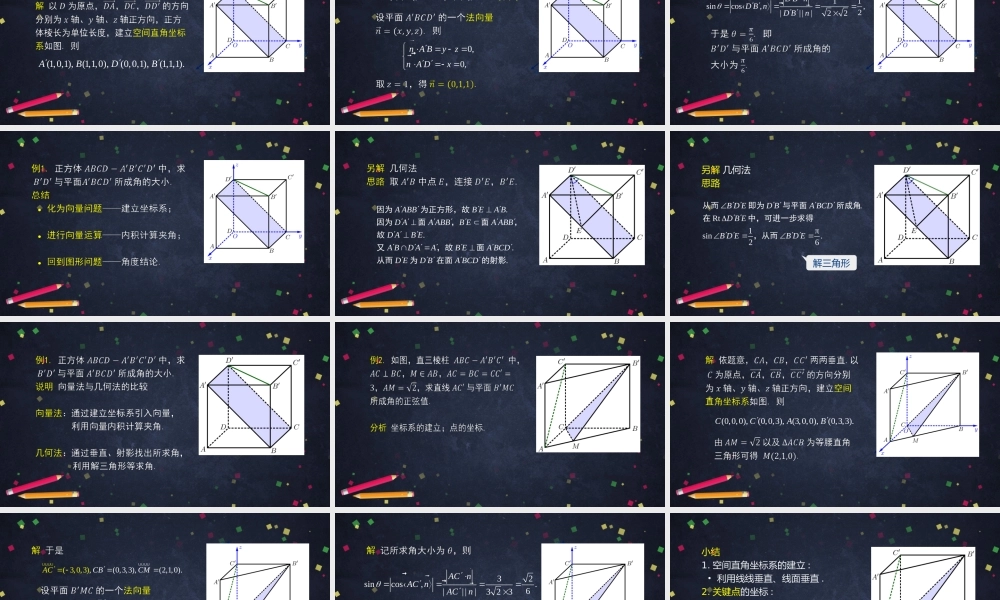
直线与平面的夹角（2）高二年级数学主讲人周康北京市第四中学北京市中小学空中课堂回忆:或ll∥定义平面的斜线与它在平面内的射影所成的锐角，称为这条斜线与平面所成的角.BAABAABBABAB是平面的斜线，斜足为，.是与平是在内的影面射所成的角.基本思路找/作射影——定/求夹角.问题如何求直线和平面的夹角？AAAA�平面是的一个法向量.向量的引入：特殊情形π.20.lnlln或∥∥向量的引入：一般情形用向量求线面角ππ,,,.22nn或sincos,.||||nnnsincos,.||||nnn(1,0,1),(1,1,0),(0,0,1),(1,1,1).ABDB(0,1,1),(1,0,0),.(1,1,0)AADDBB��0,0,nAByznADx��11sincos,,2||||22DBnDBnDBn���....AABBBEABDAAABBBEAABBDABEABDAABEABCDDEDBABCD因为为正方形，故因为面，面，故又，故面从而为在面的射影另解几何法思路.Rt1πsin.26BDEDBABCDDBEBDEBDE从而即为与平面所成角在中，可进一步求得，从而解三角形(0,0,0),(0,0,3),(3,0,0),(0,3,3).CCAB((3,.0,13(),0,3,3),2,,0)ABCCCM�330,20,nCByznCMxy��32sincos,.6||||323ACnACnACn���小结1.空间直角坐标系的建立:•利用线线垂直、线面垂直.2.关键点的坐标:借助平面几何；利用点的关系等信息.3.平面的法向量，利用方程组求解.4.向量内积的计算.线面角的应用sin303,cos3033;sin6043,cos604.BBABABABCCACACAC222(04)(330)(343)100243.BCBC�•线面角的向量呈现.•用向量法求线面角.•线面角的应用.小结sincos,.||||nnn化为向量问题进行向量运算回到图形问题教材第46页练习A3.作业1教材第46页练习B3.作业2作业3谢谢