0914高二【数学（人教B版）10】空间中的平面与空间向量（2）-课件.pptxVIP免费

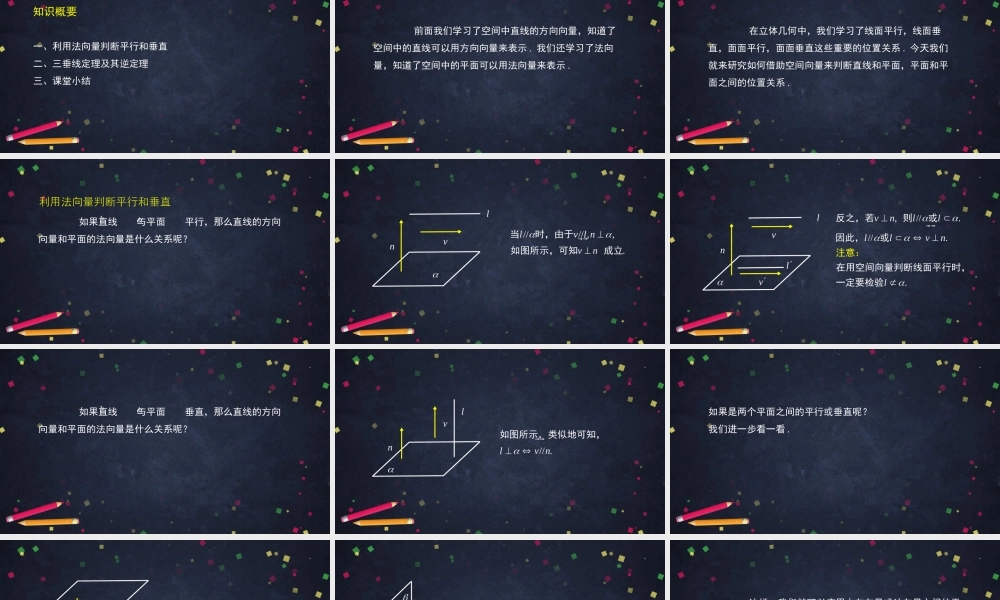
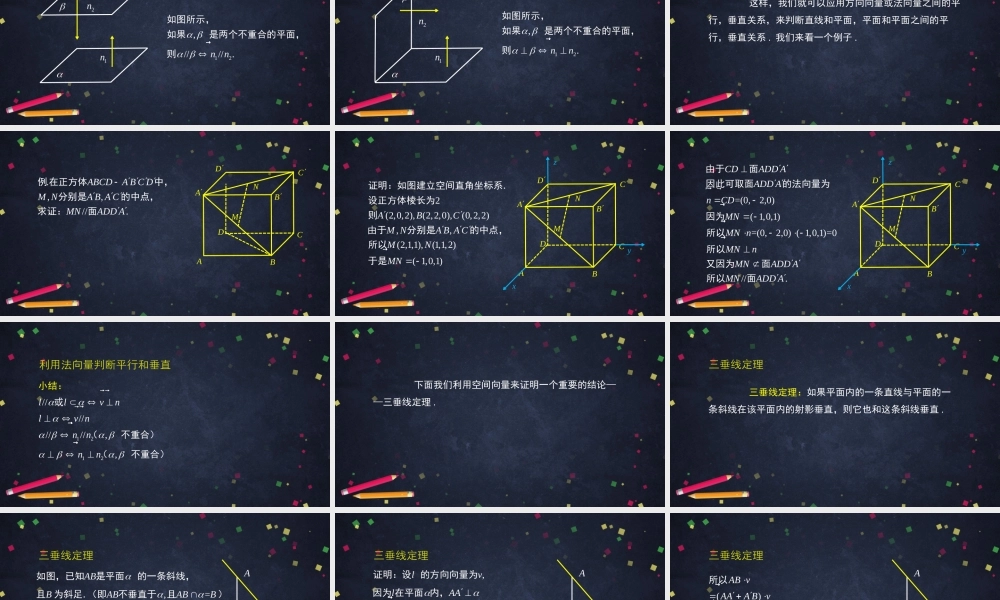
空间中的平面与空间向量（2）高二年级数学主讲人纪荣强北京市第四中学北京市中小学空中课堂知识概要一、利用法向量判断平行和垂直二、三垂线定理及其逆定理三、课堂小结前面我们学习了空间中直线的方向向量，知道了空间中的直线可以用方向向量来表示.我们还学习了法向量，知道了空间中的平面可以用法向量来表示.在立体几何中，我们学习了线面平行，线面垂直，面面平行，面面垂直这些重要的位置关系.今天我们就来研究如何借助空间向量来判断直线和平面，平面和平面之间的位置关系.如果直线与平面平行，那么直线的方向向量和平面的法向量是什么关系呢？l利用法向量判断平行和垂直vnl////,,.lvlnvn当时，由于如图所示，可知成立vnl,//.//..vnllllvnl��反之，若则或因此，或在用空间向量判断线面平行时，一定要检注意：验lv�如果直线与平面垂直，那么直线的方向向量和平面的法向量是什么关系呢？lvnl//.lvn如图所示，类似地可知，如果是两个平面之间的平行或垂直呢？我们进一步看一看.2n�1n�12,////.nn�如图所示，如果是两个不重合的平面，则2n�1n�12,.nn�如图所示，如果是两个不重合的平面，则这样，我们就可以应用方向向量或法向量之间的平行，垂直关系，来判断直线和平面，平面和平面之间的平行，垂直关系.我们来看一个例子..,,//.ABCDABCDMNABACMNADDA例在正方体中，分别是的中点，求证：面DCBAADCBNM2(2,0,2),(2,2,0),(0,2,2),,(2,1,1),(1,1,2)(1,0,1)ABCMNABACMNMN�证明：如图建立空间直角坐标系.设正方体棱长为则由于分别是的中点，所以于是DCBAADCBNMxyz=(0,2,0)(1,0,1)=(0,2,0)(1,0,1)=0//.CDADDAADDAnCDMNMNnMNnMNADDAMNADDA�����由于面因此可取面的法向量为因为所以所以又因为面所以面DCBAADCBNMxyz利用法向量判断平行和垂直1212////////,,llvnlvnnnnn��或（不重合）（不重合）小结：下面我们利用空间向量来证明一个重要的结论——三垂线定理.三垂线定理三垂线定理：如果平面内的一条直线与平面的一条斜线在该平面内的射影垂直，则它也和这条斜线垂直.,=,=..ABBABABBAAAAAAAlABlABl如图，已知是平面的一条斜...