高二【数学（人教B）16】空间中的距离（2）课件.pptxVIP免费

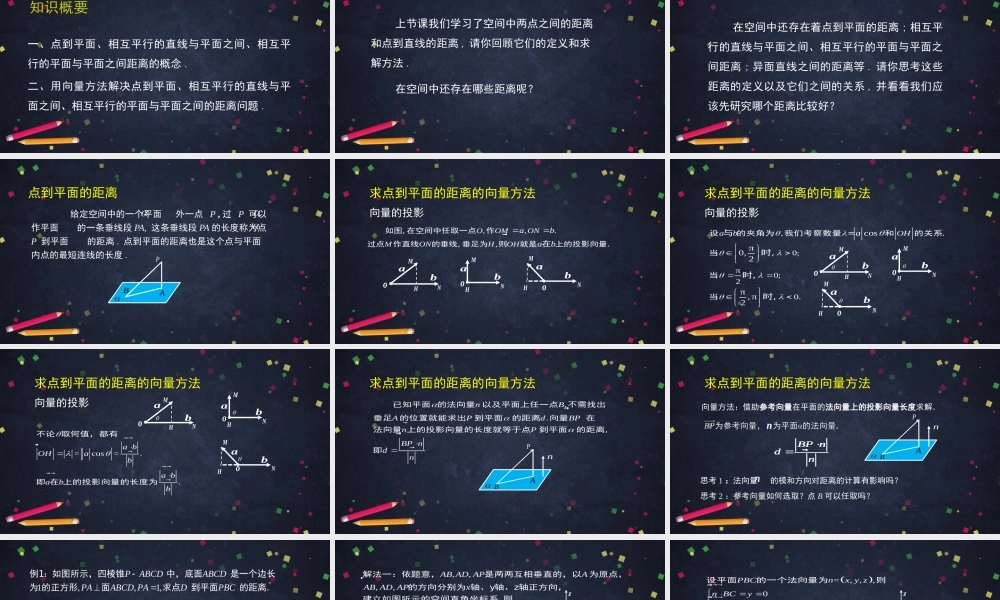
空间中的距离（2）高二年级数学主讲人吕宝珠北京市第四中学北京市中小学空中课堂一、点到平面、相互平行的直线与平面之间、相互平行的平面与平面之间距离的概念.二、用向量方法解决点到平面、相互平行的直线与平面之间、相互平行的平面与平面之间的距离问题.知识概要上节课我们学习了空间中两点之间的距离和点到直线的距离,请你回顾它们的定义和求解方法.在空间中还存在哪些距离呢？在空间中还存在着点到平面的距离;相互平行的直线与平面之间、相互平行的平面与平面之间距离;异面直线之间的距离等.请你思考这些距离的定义以及它们之间的关系,并看看我们应该先研究哪个距离比较好？点到平面的距离给定空间中的一个平面外一点P,过P可以作平面的一条垂线段PA,这条垂线段PA的长度称为点P到平面的距离.点到平面的距离也是这个点与平面内点的最短连线的长度.BAP,,,.OOMONMONHOHabab��如图,在空间中任取一点作过点作直线的垂线,垂足为则就是上的投影向量.在求点到平面的距离的向量方法向量的投影oMNHoMNHoMNHababab,0;π0;20cos.π0,2π,π.2abOHa��设的夹角为我们考察数量=和的关系当当当与时,时,时,求点到平面的距离的向量方法向量的投影oMNHbaoMNHbaoMNHba=cos=..abOHabababb�不论取何值，都有即在上的投影向量的长度为求点到平面的距离的向量方法向量的投影oMNHbaoMNHbaoMNHba,.nBAPdBPnPBPndn��已知平面的法向量以及平面上任一点不需找出垂足的位置就能求出到平面的距离向量在法向量上的投影向量的长度就等于点到平面的距离,即求点到平面的距离的向量方法BAnP向量方法：借助参考向量在平面的法向量上的投影向量长度求解．n思考2：参考向量如何选取？点B可以任取吗？思考1：法向量的模和方向对距离的计算有影响吗？BPndn��n求点到平面的距离的向量方法BAnPnBPndn��n1,,1,PABCDABCDPAABCDPADPBC例1：如图所示，四棱锥中，底面是一个边长为的正方形面求点到平面的距离.PABCD,,,1,0,0,1,1,0,0,1,0,0,0,1,0,1,0,1,0,1.AB,ADAPAABADAPxBCDPBCBP��解法一：依题意，是两两互相垂直的，以为原点，的方向分别为轴、y轴、z轴正方向，建立如图所示的空间直角坐标系.则所以PABCDxyz=,,,0011,0,=1,...