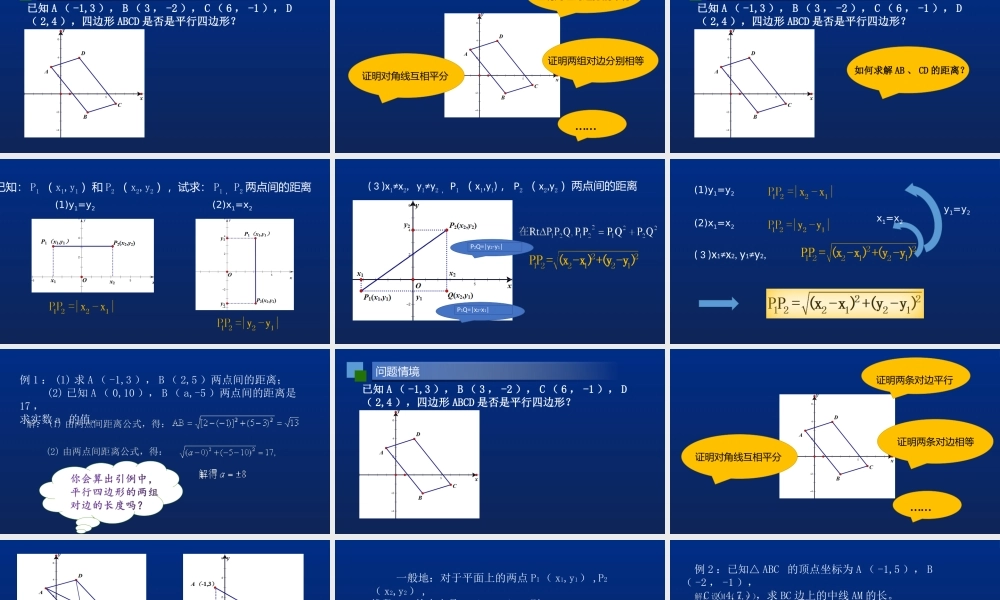
苏教版数学必修2授课教师:江苏省梅村高级中学钱佳玲指导教师:无锡市教育科学研究院张建良问题情境问题情境已知A(-1,3),B(3,-2),C(6,-1),D(2,4),四边形ABCD是否是平行四边形?证明两组对边分别平行证明两组对边分别相等证明对角线互相平分……问题情境问题情境已知A(-1,3),B(3,-2),C(6,-1),D(2,4),四边形ABCD是否是平行四边形?如何求解AB、CD的距离?已知:P1(x1,y1)和P2(x2,y2),试求:P1,P2两点间的距离(1)y1=y2(2)x1=x2P1Q=|x2-x1|P2Q=|y2-y1|(3)x1≠x2,y1≠y2,P1(x1,y1),P2(x2,y2)两点间的距离(1)y1=y2(2)x1=x2(3)x1≠x2,y1≠y2,y1=y2x1=x2例1:(1)求A(-1,3),B(2,5)两点间的距离;(2)已知A(0,10),B(a,-5)两点间的距离是17,求实数a的值。解:(1)由两点间距离公式,得:(2)由两点间距离公式,得:问题情境问题情境已知A(-1,3),B(3,-2),C(6,-1),D(2,4),四边形ABCD是否是平行四边形?证明两条对边平行证明两条对边相等证明对角线互相平分……由A1M1=M1C1,得A1C1M1所以线段AC的中点M坐标为M同理可得线段BD中点的坐标也为一般地:对于平面上的两点P1(x1,y1),P2(x2,y2),线段P1P2的中点是M(x0,y0),则例2:已知△ABC的顶点坐标为A(-1,5),B(-2,-1),C(4,7),求BC边上的中线AM的长。解:设M(x,y)即M(1,3)由两点间距离公式得:会求点A关于点B的对称点D吗?例2:已知△ABC的顶点坐标为A(-1,5),B(-2,-1),C(4,7),求BC边上的中线AM的长。会求点A关于点B的对称点D吗?解:设D(x,y)解得:x=-3,y=-7即D(-3,-7)例3、求证:点M(1,1)与点N(5,-1),关于直线l:2x-y-6=0对称分析:MNlO先求MN与l的交点O的坐标再利用两点间距离公式求证OM=ON例3、求证:点M(1,1)与点N(5,-1),关于直线l:2x-y-6=0对称变式:求点M(1,1)关于直线l:2x-y-6=0对称点。分析:证明:设MN中点为O,由中点坐标公式得O(3,0),(3,0)在直线l上,所以:所以MN被l平分;MNlO所以点M(1,1)与点N(5,-1),关于直线l:2x-y-6=0对称例3、求证:点M(1,1)与点N(5,-1),关于直线l:2x-y-6=0对称变式:求点M(1,1)关于直线l:2x-y-6=0对称点。MNlO分析:所以点M关于直线l的对称点N为(1,1)2、平面上的两点P1(x1,y1),P2(x2,y2),线段P1P2的中点是M(x0,y0)3、数学思想:从特殊到一般的数学思想,方程的思想