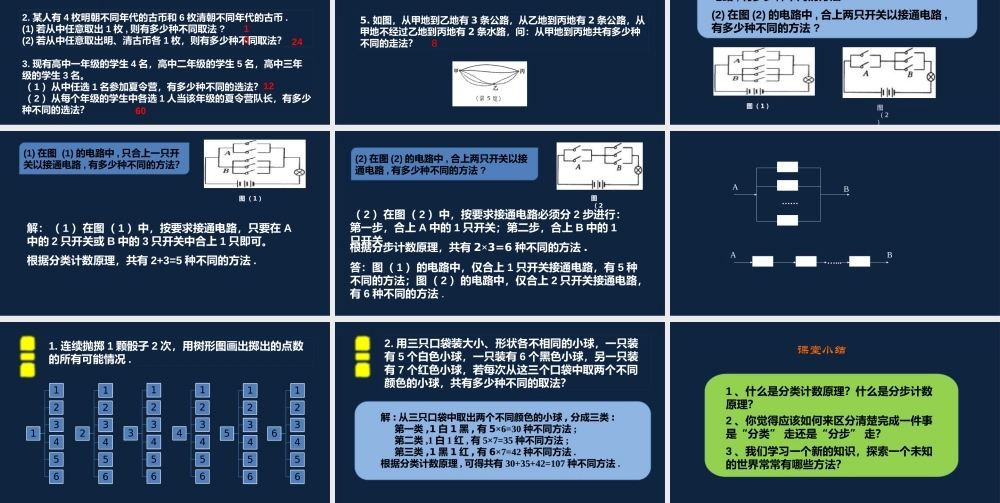
锡慧在线2020两个基本计数原理(1)苏教版选修2-3数学授课教师:江苏省锡山高级中学包东妹指导教师:惠山区教师发展中心叶亚美江苏省名师课堂问题情境1.老师的电脑设置了六位数的密码,长久不用,忘了密码,请同学们帮我解密,如果次数不限,请问:你最多需要尝试多少次?2.有一段时间,无锡的车牌号是以“苏B+一个数字+一个字母+3个数字”的形式组成,请问:这样的汽车牌照号码有多少个?如果汽车的保有量超过这个数,那么如何调整牌照号码的构成方式?生活中还有很多这样的计数问题……有待探索的自然界是有规律的,相信基本规律是简明单纯的.——爱因斯坦问题1:从南京到上海,有3条公路,2条铁路,那么从南京到上海共有多少种不同的方法?上海宁波上海如果再增加2条水路呢?完成一件事,有n类方式,在第1类方式中,有m1种不同的方法,在第2类方式中,有m2种不同的方法,……,在第n类方式中,有mn种不同的方法.那么完成这件事共有种不同的方法.N=m1+m2+…+mn分类计数原理注:本原理又称加法原理.意义建构问题2增加无锡游,从南京到无锡的路有三条,由无锡到上海的路有两条。问:从南京经无锡到上海有多少种不同的方法?上海无锡a1a2a3b1b2苏州完成一件事,需要分成n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事共有种不同的方法.注:本原理又称乘法原理.分步计数原理意义建构N=m1×m2×…×mn同:都是完成一件事,求完成这件事共有多少种不同的方法异:分类:每一类办法中的每一种方法都能完成这件事,彼此独立.分步:每一步中的每一种方法只能完成这件事的一部分,各个步骤中的各个方法相互依存,只有各个步骤都完成才算完成这件事.分类计数原理分步计数原理完成一件事,有n类方式,在第一类方式中,有m1种不同的方法,在第二类方式中,有m2种不同的方法,……,在第n类方式中,有mn种不同的方法.那么完成这件事共有N=m1+m2+…+mn种不同的方法。完成一件事,需要分成n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事共有N=m1×m2×…×mn种不同的方法。比较一下这两个原理,它们有何异同?(分门别类)(按部就班)例题举析例1某班共有男生28名,女生20名,从该班选出学生代表参加校学代会.(1)若学校分配给该班1名代表,有多少种不同的选法?(2)若学校分配给该班2名代表,且男女生代表各1名,有多少种不同的选法?解:答:选出1名代表有48种不同...