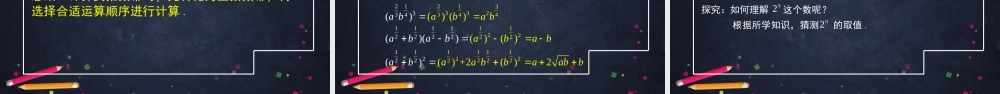1028高一【数学(人教B版)】实数指数幂及其运算-课件.pptxVIP免费

实数指数幂及其运算高一年级数学主讲人任爽北京师范大学附属中学北京市中小学空中课堂为了解决类似情境中的问题，需要进一步学习指数运算.温故知新回顾初中所学的整数指数幂相关知识：1.正整数指数幂：一般地，（个相乘，），其中称为底数，称为指数，叫的次幂.零指数幂：（）.负整数指数幂：....naaaaanan*Nannaan01a0a-n1naa温故知新例如：正整数指数幂：0指数幂：负整数指数幂：5222222=32021-33112=28温故知新2.你还记得整数指数幂有哪些运算法则吗？（1）（2）（3）（4）mnmnaaamnmnaa（）mmnnaaammmabab（）温故知新回顾初中所学的平方根和立方根知识：1.平方根：如果，则称为的平方根（或二次方根）.当时，有两个平方根，它们互为相反数；正的平方根为负的平方根为.当时，只有一个平方根，记为.当时，在实数范围内没有平方根.2xaxa0aaaa=0aa0=00aa温故知新你还记得二次根式有哪些运算法则吗？（1）（2）（3）2aa（）aabbabab温故知新2.立方根：如果，则称为的立方根（或三次方根）.在实数范围内，任意实数有且只有一个立方根，记为..3xaxa3aa概念推广复习了平方根和立方根的概念后，你能类比给出四次方根、五次方根的定义，进而得到n次方根的定义吗？得到新知n次方根的定义:一般地,给定大于1的正整数n和实数，如果存在实数,使得，则称为的n次方根.axnxaax尝试与发现通过的解的情况，参考平方根与立方根的特征，你能归纳出n次方根的一些特征吗？如：nxa481x532x尝试与发现奇数偶数a=0a>0有且只有一个，记作：，是一个正数.有两个，它们互为相反数，记为和a<0有且只有一个，记作：，是一个负数.实数范围内不存在被开方数a根指数n00nnananana得到新知根式定义：当有意义时，称为根式，n称为根指数，称为被开方数.那么，你能根据n次方根的上述特征得到根式的运算性质吗？如：anana5-2得到新知根式的运算性质：（1）（2）当n为奇数时，；当n为偶数时，.练习：nnaa（）nnaannaa5352（）772)（443)（333282思考与发现复习了整数指数幂的运算和根式的概念与运算以后，我们来将其推广到分数指数幂运算，即给出等的定义,我们希望推广后相关运算性质仍然保持,如,在m、n都是分数时仍然成立，是否可以呢？125mnmnaa（）尝试与发现计算比较下面两组算式，看看有什么发现？1.,；,.2.,；,.发现：每组式子中的计算结果相同，所以根式可转化为分数指数幂...