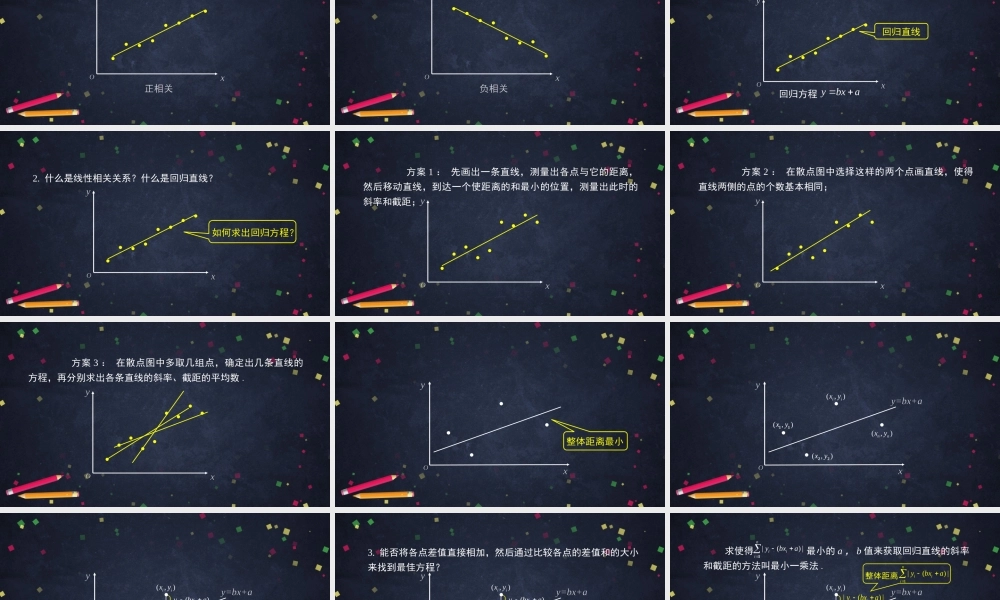
回归分析的基本思想及其初步应用(1)高二年级数学主讲人:刘阳北京市第十二中学钱学森学校(1)正方体的体积与边长之间的关系;1.下列变量之间的关系哪些是函数关系?哪些是相关关系?(3)商品销售收入与广告支出经费之间的关系;(4)人体内的脂肪含量与年龄之间的关系.(2)某人骑行了1km,他骑车的平均速度与骑行时间之间的关系;知识概要(1)正方体的体积与边长之间的关系;1.下列变量之间的关系哪些是函数关系?哪些是相关关系?(3)商品销售收入与广告支出经费之间的关系;(4)人体内的脂肪含量与年龄之间的关系.(2)某人骑行了1km,他骑车的平均速度与骑行时间之间的关系;知识概要(1)、(2)是函数关系.(1)正方体的体积与边长之间的关系;1.下列变量之间的关系哪些是函数关系?哪些是相关关系?(3)商品销售收入与广告支出经费之间的关系;(4)人体内的脂肪含量与年龄之间的关系.(2)某人骑行了1km,他骑车的平均速度与骑行时间之间的关系;知识概要(3)、(4)是相关关系.对于两个变量,当自变量取值一定时,因变量的值也确定,则为函数关系,函数关系是一种确定性关系;当自变量取值一定时,因变量的取值带有随机性,则为相关关系,相关关系是一种非确定性关系.xyO散点图xyOxyO函数关系xyOxyO相关关系xyO正相关xyO负相关2.什么是线性相关关系?什么是回归直线?xyO回归直线ybxa回归方程2.什么是线性相关关系?什么是回归直线?xyO如何求出回归方程?方案1:先画出一条直线,测量出各点与它的距离,然后移动直线,到达一个使距离的和最小的位置,测量出此时的斜率和截距;xyOxyO方案2:在散点图中选择这样的两个点画直线,使得直线两侧的点的个数基本相同;方案3:在散点图中多取几组点,确定出几条直线的方程,再分别求出各条直线的斜率、截距的平均数.xyO整体距离最小xOyy=bx+axO(,)nnxy(,)xy11(,)xy22(,)iixyyy=bx+a(,)nnxyxO}}(,)xy11(,)xy22(,)iixy()iiybxay3.能否将各点差值直接相加,然后通过比较各点的差值和的大小来找到最佳方程?y=bx+a(,)nnxyxO}}(,)xy11(,)xy22(,)iixy()iiybxayxyO}}(,)xy11(,)xy22(,)iixyy=bx+a(,)nnxy求使得最小的a,b值来获取回归直线的斜率和截距的方法叫最小一乘法.|()|niiiybxa11|()|niiiybxa整体距离|()|iiybxay=bx+a(,)nnxy4.要确定线性回归方程,“最小一乘法”是不是唯一的方法?你能否想到其它的判定标准?xO}}(,)xy11(,)xy22(,)iixyy1|()|niiiyb...