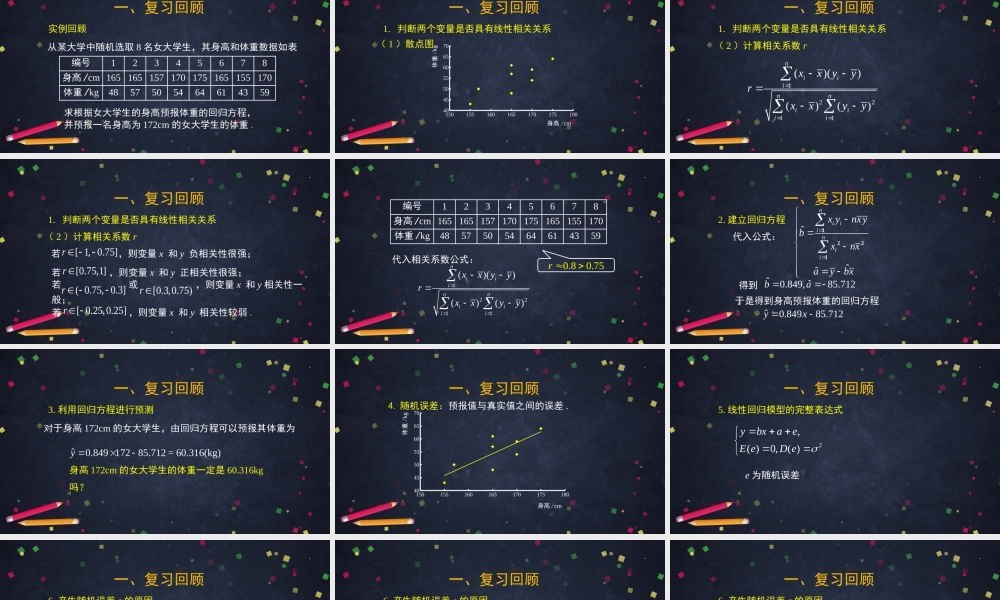
主讲人:杨春武北京市第十中学回归分析的基本思想及其初步应用(2)高二年级数学从某大学中随机选取8名女大学生,其身高和体重数据如表编号12345678身高/cm165165157170175165155170体重/kg4857505464614359一、复习回顾实例回顾求根据女大学生的身高预报体重的回归方程,并预报一名身高为172cm的女大学生的体重.15015516016517017518040455055606570身高/cm体重/kg1.判断两个变量是否具有线性相关关系一、复习回顾(1)散点图一、复习回顾12211()()()()niiinniiiixxyyrxxyy(2)计算相关系数r1.判断两个变量是否具有线性相关关系一、复习回顾(2)计算相关系数r1.判断两个变量是否具有线性相关关系若,则变量x和y负相关性很强;[1,0.75]r若,则变量x和y正相关性很强;[0.75,1]r若或,则变量x和y相关性一般;(0.75,0.3]r[0.3,0.75)r若,则变量x和y相关性较弱.[0.25,0.25]r12211()()()()niiinniiiixxyyrxxyy代入相关系数公式:0.80.75r编号12345678身高/cm165165157170175165155170体重/kg4857505464614359代入公式:得到ˆˆ0.849,85.712ba于是得到身高预报体重的回归方程ˆ0.84985.712yx-2.建立回归方程一、复习回顾ˆˆˆniiiniixynxybxnxaybx12213.利用回归方程进行预测一、复习回顾对于身高172cm的女大学生,由回归方程可以预报其体重为身高172cm的女大学生的体重一定是60.316kg吗?ˆ0.84917285.712=60.316(kg)y-15015516016517017518040455055606570身高/cm体重/kg一、复习回顾4.随机误差:预报值与真实值之间的误差.5.线性回归模型的完整表达式一、复习回顾e为随机误差2,()0,()ybxaeEeDe一、复习回顾(1)用线性回归模型近似真实模型所引起的误差真实模型是客观存在的,通常我们并不知道真实模型到底是什么,可能存在非线性的函数能够更好地描述y与x之间的关系,但是现在却用线性函数来表示这种关系,结果就会产生误差.这种由于模型近似所引起的误差包含在e中.6.产生随机误差e的原因一、复习回顾(2)忽略了某些因素的影响影响变量y的因素不只变量x一个,可能还包括其他许多因素.例如在描述身高和体重关系的模型中,体重不仅受身高的影响,还会受遗传基因、饮食习惯、生长环境等其他因素的影响,但通常它们每一个因素的影响可能都是比较小的,它们的影响都体现在e中.6.产生随机误差e的原因一、复习...