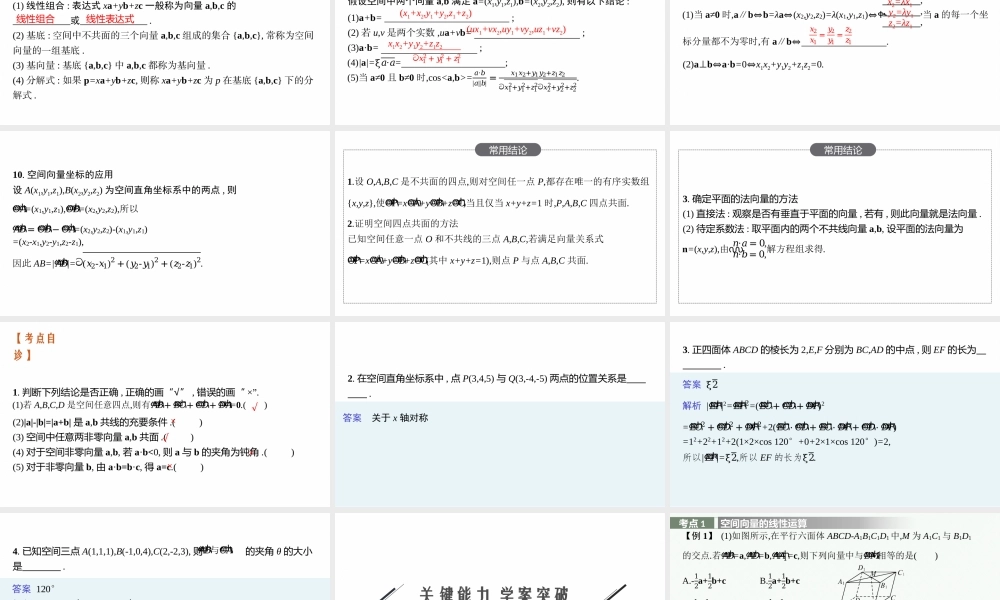
高考总复习优化设计GAOKAOZONGFUXIYOUHUASHEJI7.5空间向量及其运算第七章2022内容索引0102必备知识预案自诊关键能力学案突破必备知识预案自诊【知识梳理】1.空间向量(1)定义:空间中既有又有的量称为空间向量.(2)向量的模(或长度):向量的.(3)表示方法:①几何表示法:可以用来直观的表示向量,如始点为A终点为B的向量,记为,向量的模用表示.②字母表示法:可以用加粗的斜体小写字母a,b,c来表示向量,向量a的模用|a|或|𝑎→|来表示.𝐴𝐵ሬሬሬሬሬԦ|𝐴𝐵ሬሬሬሬሬԦ|大小方向大小有向线段2.几类特殊的向量名称定义零向量和相同的向量称为零向量,记作0单位向量模等于的向量称为单位向量相等向量大小、方向的向量称为相等向量相反向量方向、大小的向量称为相反向量平行向量方向相同或者相反的两个非零向量互相,此时表示这两个非零向量的有向线段所在的直线或重合.通常规定零向量与任意向量平行共面向量一般地,空间中的多个向量,如果表示它们的有向线段通过平移后,都能在内,则称这些向量共面始点终点1相等相同相反相等平行平行同一平面3.空间向量的线性运算(1)给定两个平面向量a,b,在该平面内任取一点A,作𝐴𝐵ሬሬሬሬሬԦ=a,𝐵𝐶ሬሬሬሬሬԦ=b,作出向量𝐴𝐶ሬሬሬሬሬԦ,则𝐴𝐶ሬሬሬሬሬԦ是向量a与b的和(也称𝐴𝐶ሬሬሬሬሬԦ为向量a与b的和向量).向量a与b的和向量记作a+b,因此𝐴𝐵ሬሬሬሬሬԦ+𝐵𝐶ሬሬሬሬሬԦ=𝐴𝐶ሬሬሬሬሬԦ.在空间中任取一点O,作𝑂𝐴ሬሬሬሬሬԦ=a,𝑂𝐵ሬሬሬሬሬԦ=b,作出向量𝐵𝐴ሬሬሬሬሬԦ,则向量𝐵𝐴ሬሬሬሬሬԦ就是向量a与b的差(也称𝐵𝐴ሬሬሬሬሬԦ为向量a与b的差向量),即𝑂𝐴ሬሬሬሬሬԦ−𝑂𝐵ሬሬሬሬሬԦ=𝐵𝐴ሬሬሬሬሬԦ.(2)𝐷𝐴ሬሬሬሬሬԦ+𝐷𝐶ሬሬሬሬሬԦ+𝐷𝐷1ሬሬሬሬሬሬሬሬԦ=.即三个不共面向量的和,等于以这三个向量为邻边的平行六面体中,与这三个向量有所表示的向量.(3)给定一个实数λ与任意一个空间向量a,则实数λ与空间向量a相乘的运算称为数乘向量,记作λa.其中:①当λ≠0且a≠0时,λa的模为,而且λa的方向:(ⅰ)当λ>0时,与a的方向;(ⅱ)当λ<0时,与a的方向.②当λ=0或a=0时,λa=.(4)空间向量的线性运算满足如下运算律:对于实数λ与μ,向量a与b,有λa+μa=(λ+μ)a,λ(a+b)=λa+λb.𝐷𝐵1ሬሬሬሬሬሬሬሬԦ共同始点的对角线|λ||a|相同相反04.空间向量的数量积(1)空间向量的夹角如果
=π2,则称向量a,b,记作a⊥b.非零∠AOB[0,π]互相垂直(2)空间向量数量积的定义:两个非零向量a,b的数量...