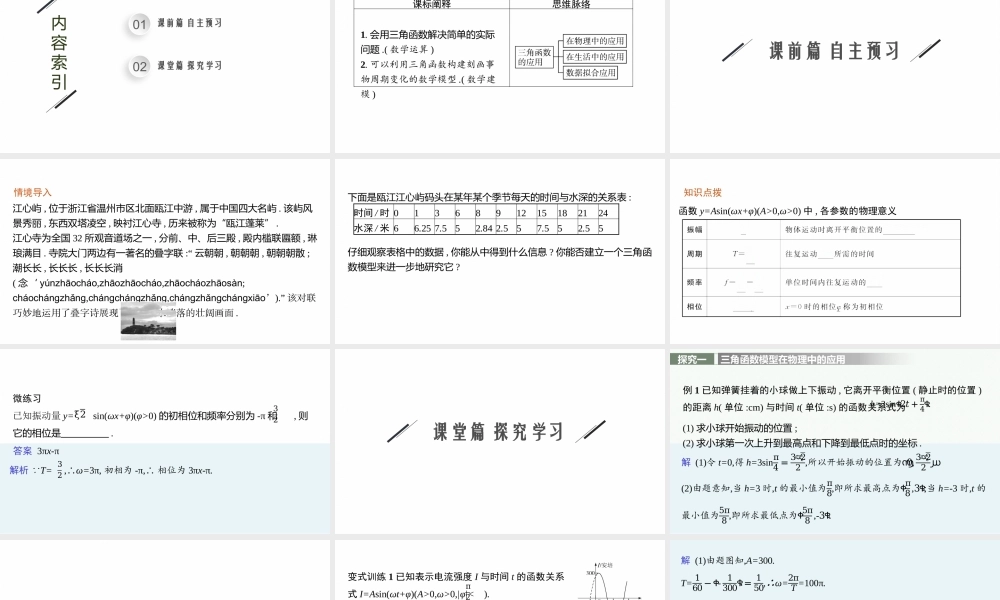
高中同步学案优化设计GAOZHONGTONGBUXUEANYOUHAUSHEJI7.4三角函数的应用第7章2021内容索引0102课前篇自主预习课堂篇探究学习课标阐释思维脉络1.会用三角函数解决简单的实际问题.(数学运算)2.可以利用三角函数构建刻画事物周期变化的数学模型.(数学建模)课前篇自主预习情境导入江心屿,位于浙江省温州市区北面瓯江中游,属于中国四大名屿.该屿风景秀丽,东西双塔凌空,映衬江心寺,历来被称为“瓯江蓬莱”.江心寺为全国32所观音道场之一,分前、中、后三殿,殿内槛联匾额,琳琅满目.寺院大门两边有一著名的叠字联:“云朝朝,朝朝朝,朝朝朝散;潮长长,长长长,长长长消(念‘yúnzhāocháo,zhāozhāocháo,zhāocháozhāosàn;cháochángzhǎng,chángchángzhǎng,chángzhǎngchángxiāo’).”该对联巧妙地运用了叠字诗展现了瓯江潮水涨落的壮阔画面.下面是瓯江江心屿码头在某年某个季节每天的时间与水深的关系表:时间/时0136891215182124水深/米66.257.552.842.557.552.55仔细观察表格中的数据,你能从中得到什么信息?你能否建立一个三角函数模型来进一步地研究它?知识点拨函数y=Asin(ωx+φ)(A>0,ω>0)中,各参数的物理意义微练习已知振动量y=sin(ωx+φ)(φ>0)的初相位和频率分别为-π和,则它的相位是.ξ232答案3πx-π解析 T=,∴ω=3π,初相为-π,∴相位为3πx-π.32课堂篇探究学习探究一三角函数模型在物理中的应用例1已知弹簧挂着的小球做上下振动,它离开平衡位置(静止时的位置)的距离h(单位:cm)与时间t(单位:s)的函数关系式为h=3sinቀ2𝑡+π4ቁ.(1)求小球开始振动的位置;(2)求小球第一次上升到最高点和下降到最低点时的坐标.解(1)令t=0,得h=3sinπ4=3ඥ22,所以开始振动的位置为൬0,3ඥ22൰.(2)由题意知,当h=3时,t的最小值为π8,即所求最高点为ቀπ8,3ቁ;当h=-3时,t的最小值为5π8,即所求最低点为ቀ5π8,-3ቁ.反思感悟利用三角函数处理物理学问题的策略(1)常涉及的物理学问题有单摆,光波,电流,机械波等,其共同的特点是具有周期性.(2)明确物理概念的意义,此类问题往往涉及诸如频率、振幅等概念,因此要熟知其意义并与对应的三角函数知识结合解题.变式训练1已知表示电流强度I与时间t的函数关系式I=Asin(ωt+φ)(A>0,ω>0,|φ|<).(1)若电流强度I与时间t的函数关系图象如图所示,试根据图象写出I=Asin(ωt+φ)的解析式;π2(2)为了使I=Asin(ωt+φ)ቀ𝐴>0,𝜔>0,|𝜑|<π2ቁ中t在任意一段1100秒的时间内电流强度I能同时取得最大值A与最小值-A,则正整数ω的最小...