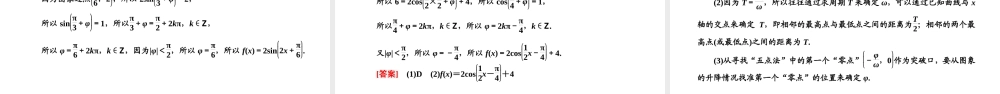5.6 函数y=Asin（ωx+φ）.pptxVIP免费

5.6函数y＝Asin(ωx＋φ)明确目标发展素养1.了解y＝Asin(ωx＋φ)的实际意义．2.能借助图象理解参数ω，φ，A的意义，了解参数的变化对函数图象的影响.1.通过函数图象的变换，培养直观想象素养．2.借助函数的图象求解析式，提升数学运算素养.(一)教材梳理填空(1)φ对y＝sin(x＋φ)，x∈R的图象的影响：(2)ω(ω＞0)对y＝sin(ωx＋φ)的图象的影响：(3)A(A＞0)对y＝Asin(ωx＋φ)的图象的影响：(二)基本知能小试1．判断正误(1)由函数y＝sinx－π3的图象得到y＝sinx的图象，必须向左平移．()(2)把函数y＝sinx的图象上点的横坐标伸长到原来的3倍就得到函数y＝sin3x的图象．()(3)在进行函数y＝Asin(ωx＋φ)图象间变换的时候必须先左右平移，再进行伸缩变换．()答案：(1)×(2)×(3)×2．把函数y＝sinx的图象向左平移π3个单位长度后所得图象的解析式为()A．y＝sinx－π3B．y＝sinx＋π3C．y＝sinx－π3D．y＝sinx＋π3解析：根据图象变换的方法，y＝sinx的图象向左平移π3个单位长度后得到y＝sinx＋π3的图象．答案：D3．函数y＝Asin(ωx＋φ)＋1(A>0，ω>0)的最大值为5，则A的值为()A．5B．－5C．4D．－4解析：因为A>0，所以当sin(ωx＋φ)＝1时，ymax＝A＋1＝5，所以A＝4.答案：C4．函数y＝sinx＋1的对称中心坐标为________．解析：函数y＝sinx＋1的对称中心坐标为(kπ，1)，k∈Z.答案：(kπ，1)，k∈Z题型一三角函数图象之间的变换【学透用活】[典例1]已知函数y＝f(x)的图象上的每一点的纵坐标扩大到原来的4倍，横坐标扩大到原来的2倍，然后把所得的图象沿x轴向左平移π2个单位长度，这样得到的曲线和y＝2sinx的图象相同，则函数y＝f(x)的解析式为_______．[解析][答案]f(x)＝－12cos2x[方法技巧]三角函数图象平移变换问题的关键及解题策略(1)确定函数y＝sinx的图象经过平移变换后图象对应的解析式，关键是明确左右平移的方向，即按“左加右减”的原则进行．(2)已知两个函数解析式判断其图象间的平移关系时，首先要将解析式化为同名三角函数形式，然后再确定平移方向和单位．【对点练清】1．将函数y＝2cos2x＋π3的图象向左平移π3个单位长度，再向下平移3个单位长度，则所得图象的解析式为_______．解析：y＝2cos2x＋π3的图象向左平移π3个单位长度，得y＝2cos2x＋π3＋π3＝2cos(2x＋π)＝－2cos2x，再向下平移3个单位长度得y＝－2cos2x－3的...