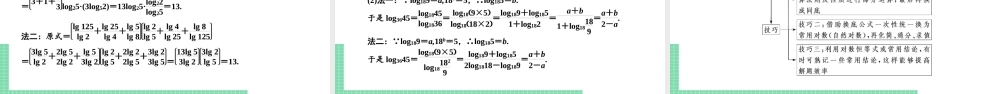4.3.2对数的运算（课件）.pptxVIP免费

高中数学必修第一册RJRJA精品教学课件4.3.2对数的运算4.3.2对数的运算1．理解对数的运算性质．2．知道用换底公式能将一般对数转化成自然对数或常用对数．3．通过对数的运算性质及换底公式的掌握提升学生数学抽象的核心素养，会用对数的运算性质进行化简求值，进一步提升学生数学运算的核心素养．知识点一对数的运算性质(一)教材梳理填空若a>0，且a≠1，M>0，N>0，那么：(1)loga(MN)＝______________；(2)logaMN＝_____________；(3)logaMn＝_______(n∈R)．logaM＋logaNlogaM－logaNnlogaM[提醒]对数与指数运算对照表(a＞0，且a≠1，m＞0，N＞0)式子ab＝NlogaN＝bam·an＝am＋nloga(MN)＝logaM＋logaNaman＝am－nlogaMN＝logaM－logaN运算性质(am)n＝amnlogaMn＝nlogaM(二)基本知能小试1．判断正误(1)log2x2＝2log2x.()(2)loga[(－2)×(－3)]＝loga(－2)＋loga(－3)．()(3)loga(xy)＝logax·logay.()(4)log2(－5)2＝2log2(－5)．()答案：(1)×(2)×(3)×(3)×2．计算log84＋log82等于()A．log86B．8C．6D．1答案：D3．log1327－log139＝________.答案：－14．2lg4＋lg58＝________.答案：1知识点二换底公式(一)教材梳理填空logab＝_______(a＞0，且a≠1；b＞0；c＞0，且c≠1)．我们把上式叫做对数换底公式．logcblogca提示：是大于0且不等于1的任意数．[思考]换底公式中底数c是特定数还是任意数？(二)基本知能小试1．判断正误(1)由换底公式可得logab＝log－2blog－2a.()(2)log2M＋log3N＝log6(MN)．()(3)log23·log32＝1.()答案：(1)×(2)×(3)√2．填空：(1)logab·logba＝________；(2)logab·logbx＝________；(3)logamNn＝________.答案：(1)1(2)logax(3)nmlogaN3．log23·log34·log42＝________.解析：log23·log34·log42＝lg3lg2·lg4lg3·lg2lg4＝1.答案：1题型一对数运算性质的应用[学透用活]1．对数运算性质的适用前提对数的运算性质的适用条件是“同底，且真数为正”，即a＞0，a≠1，M＞0，N＞0.若去掉此条件，性质不一定成立．2．对数运算性质(1)的推广性质(1)可以推广到若干个正因数的积：loga(M1·M2·M3·…·Mn)＝logaM1＋logaM2＋…＋logaMn(a＞0，且a≠1，Mi＞0，i＝1,2，…，n)．[典例1](1)若lg2＝a，lg3＝b，则lg12lg15＝()A.2a＋b1－a＋bB．2a＋b1＋a＋bC.a＋2b1－a＋bD．a＋2b1＋a＋b(2)①(lg5)2＋2lg2－(lg2)2；②lg3＋25lg9＋35lg27－lg3lg81－lg27；③log535－2log573＋log57－log51.8.[解析](1)选Alg12lg15＝lg...