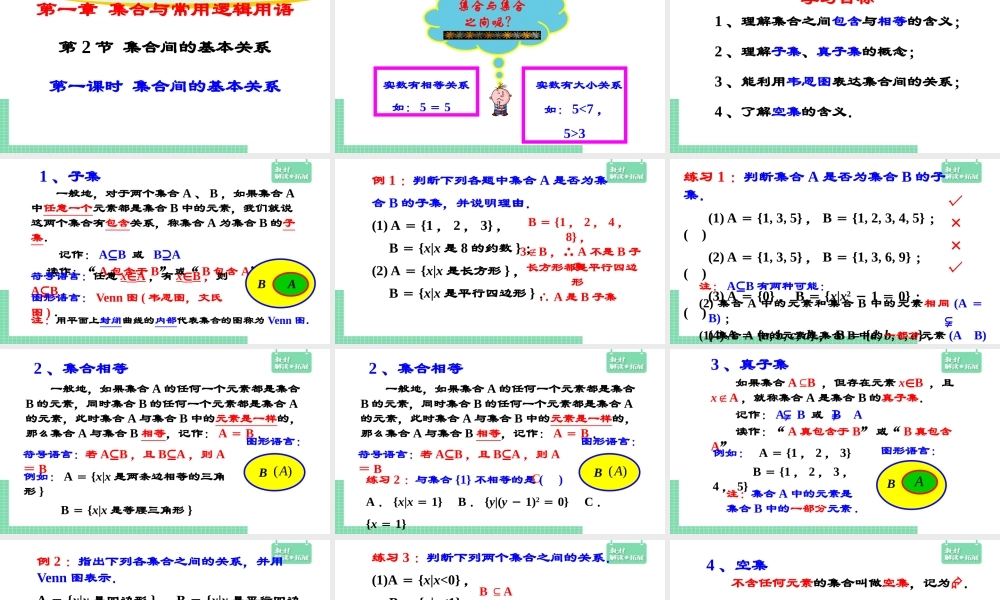
高中数学必修第一册RJRJA精品教学课件第一章集合与常用逻辑用语第2节集合间的基本关系第一课时集合间的基本关系实数有大小关系如:5<7,5>3实数有相等关系如:5=5集合与集合之间呢?学习目标1、理解集合之间包含与相等的含义;2、理解子集、真子集的概念;3、能利用韦恩图表达集合间的关系;4、了解空集的含义.1、子集一般地,对于两个集合A、B,如果集合A中任意一个元素都是集合B中的元素,我们就说这两个集合有包含关系,称集合A为集合B的子集.记作:A⊆B或B⊇A读作:“A包含于B”或“B包含A”符号语言:任意x∈A,有x∈B,则A⊆B.BA图形语言:Venn图(韦恩图,文氏图).注:用平面上封闭曲线的内部代表集合的图称为Venn图.例1:判断下列各题中集合A是否为集合B的子集,并说明理由.(1)A={1,2,3},B={x|x是8的约数};(2)A={x|x是长方形},B={x|x是平行四边形}.B={1,2,4,8},3∉B,∴A不是B子集长方形都是平行四边形∴A是B子集练习1:判断集合A是否为集合B的子集.(1)A={1,3,5},B={1,2,3,4,5};()(2)A={1,3,5},B={1,3,6,9};()(3)A={0},B={x|x2-1=0};()(4)A={a,b,c,d},B={d,b,c,a}.×√×√注:A⊆B有两种可能:(2)集合A中的元素和集合B中的元素相同(A=B);(1)集合A中的元素是集合B中的一部分元素(AB)⊂≠2、集合相等一般地,如果集合A的任何一个元素都是集合B的元素,同时集合B的任何一个元素都是集合A的元素,此时集合A与集合B中的元素是一样的,那么集合A与集合B相等,记作:A=B.例如:A={x|x是两条边相等的三角形}B={x|x是等腰三角形}B)(A符号语言:若A⊆B,且B⊆A,则A=B图形语言:2、集合相等一般地,如果集合A的任何一个元素都是集合B的元素,同时集合B的任何一个元素都是集合A的元素,此时集合A与集合B中的元素是一样的,那么集合A与集合B相等,记作:A=B.练习2:与集合{1}不相等的是()A.{x|x=1}B.{y|(y-1)2=0}C.{x=1}B)(A符号语言:若A⊆B,且B⊆A,则A=B图形语言:C3、真子集如果集合A⊆B,但存在元素x∈B,且xA∉,就称集合A是集合B的真子集.记作:AB或BA读作:“A真包含于B”或“B真包含A”例如:A={1,2,3}B={1,2,3,4,5}BA注:集合A中的元素是集合B中的一部分元素.⊂≠≠⊃图形语言:例2:指出下列各集合之间的关系,并用Venn图表示.A={x|x是四边形},B={x|x是平行四边形};C={x|x是矩形},D={x|x是正方形}.D⊆C⊆BA⊆DCBA⊂≠⊂≠⊂≠ABCD练习3:判断下列两个集合之...