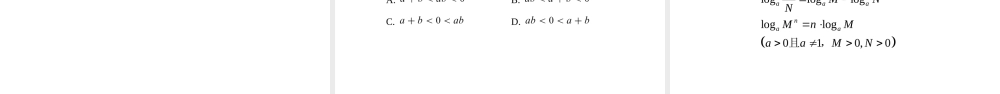1 函数专题讲座 南开中学 林秋莎.pptxVIP免费

空白演示函数专题讲座天津市南开中学林秋莎（一）函数的图象和性质（二）比较大小问题（三）零点问题（四）参数问题（一）函数的图象和性质（二）比较大小问题（三）零点问题（四）参数问题（一）函数的图象和性质（二）比较大小问题（三）零点问题（四）参数问题单调性奇偶性周期性函数的性质1.2.3.单调性1.12212121,,,,.xxfxfyfxIDIxxDfxDDfxfxDDfxxfxfx函数的定义域为区间且若，就说在上是增函数，区间叫做函数的增区间；若，就说在上是减函数，区间叫做函数的减区间.奇偶性2..,,yfxIxIfxIxIfxfxfxxfxIf函数的定义域为若有，则为上的奇函数；若有，则为上的偶函数.◆奇函数的图象关于坐标原点中心对称◆偶函数的图象关于y轴轴对称事半功倍！！！周期性3.,yfxIxIfxITyfxTTyfTfxTfxx函数的定义域为若存在，使得对于，总有成立，则称为上的周期函数，叫做函数的周期.若存在最小正数满足上非零常述定义，则称为函数的数最小正周期.（一）函数的图象和性质（二）比较大小问题（三）零点问题（四）参数问题A.B.C.D.2ee2018IIxxfxx例（全国）函数的图象大致为（）.1（一）函数的图象和性质（二）比较大小问题（三）零点问题（四）参数问题BA.B.C.D.22ee11e0e,e,e0,,.xxxxfxxfxfxfxxfx设，奇函数2ee2018IIxxfxx例（全国）函数的图象大致为（）.1（一）函数的图象和性质（二）比较大小问题（三）零点问题（四）参数问题20182sin2xfxx例2（浙江）函数的图象可能是（）.A.B.C.D.（一）函数的图象和性质（二）比较大小问题（三）零点问题（四）参数问题DA.B.C.D.3π3π443π3π2sin2042fxfxf，奇函数20182sin2xfxx例（浙江）函数的图象可能是（）.2（一）函数的图象和性质（二）比较大小问题（三）零点问题（四）参数问题A.B.C.D.22016I2e2,2xyx例（全国）函数在的图象大致为（）.3（一）函数的图象和性质（二）比较大小问题（三）零点问题（四）参数问题A.B.C.D.D222e0112e0,028e10'4e'010,'14e>0xxfxxfxfxfffxfxxff设，偶函数当时，22016I2e2,2xyx例（全国...