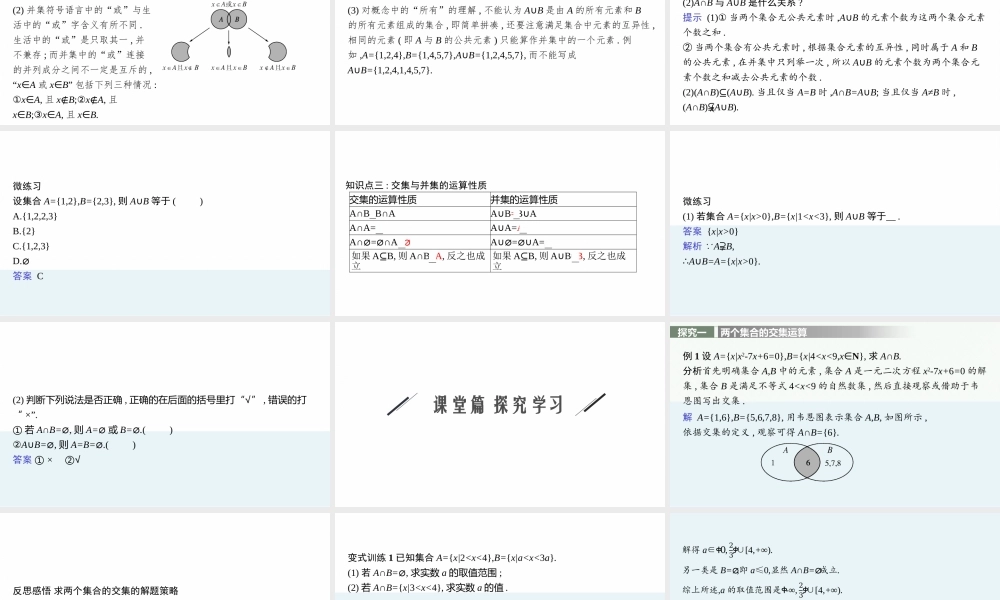
高中同步学案优化设计GAOZHONGTONGBUXUEANYOUHAUSHEJI1.1.3集合的交与并第1章2021内容索引0102课前篇自主预习课堂篇探究学习课标阐释思维脉络1.理解两个集合的交集与并集的含义.(数学抽象)2.会求两个集合的交集与并集.(数学运算)3.能使用韦恩图或数轴表达集合之间的运算,体会图形对理解抽象概念的作用.(直观想象)课前篇自主预习情境导入某单位食堂第一天买菜的品种构成的集合记为A={黄瓜,冬瓜,鲫鱼,虾,茄子};第二天买菜的品种构成的集合记为B={黄瓜,猪肉,毛豆,芹菜,虾,土豆}.问:1.两天所买过的相同菜的品种构成的集合记为C,则集合C等于什么?2.两天买过的所有菜的品种构成的集合记为D,则集合D等于什么?知识梳理知识点一:两个集合的交名师点析1.对交集概念的理解(1)对于“A∩B={x|x∈A且x∈B}”,包含以下两层意思:①A∩B中的任一元素都是A与B的公共元素;②A与B的公共元素都属于A∩B,这就是文字定义中“所有”二字的含义,如A={1,2,3},B={2,3,4},则A∩B={2,3},而不是{2}或{3}.(2)当A=B时,A∩B=A和A∩B=B同时成立.2.求两集合交集的注意点(1)求两集合的交集时,首先要化简集合,使集合元素的性质特征尽量明显化,然后根据交集的含义写出结果.(2)在求与不等式有关的集合的交集运算时,数轴分析法直观清晰,因此应重点考虑.微思考两个非空集合的交集可能是空集吗?提示两个非空集合的交集可能是空集,即A与B无公共元素时,A与B的交集仍然存在,只不过这时A∩B=⌀.反之,若A∩B=⌀,则A,B这两个集合可能至少有一个为空集,也可能这两个集合都是非空的,如A={1,3,5,7,9},B={2,4,6,8,10},此时A∩B=⌀.微练习已知集合M={x|-2≤x<2},N={0,1,2},则M∩N等于()A.{0}B.{1}C.{0,1,2}D.{0,1}答案D解析按照交集的定义求解即可.M∩N={x|-2≤x<2}∩{0,1,2}={0,1}.知识点二:两个集合的并名师点析对并集的理解(1)A∪B仍是一个集合,A∪B由所有属于集合A或属于集合B的元素组成.(2)并集符号语言中的“或”与生活中的“或”字含义有所不同.生活中的“或”是只取其一,并不兼存;而并集中的“或”连接的并列成分之间不一定是互斥的,“x∈A或x∈B”包括下列三种情况:①x∈A,且x∉B;②x∉A,且x∈B;③x∈A,且x∈B.(3)对概念中的“所有”的理解,不能认为A∪B是由A的所有元素和B的所有元素组成的集合,即简单拼凑,还要注意满足集合中元素的互异性,相同的元素(即A与B的公共元素)只能算作并集中的一个元素.例如,A={1,2,4},B={1,4,5,7},A∪B={1,2,4,5,7},而不能写成A∪B={1,2,4,1,4,5,7}.微思考(1)集合A∪...