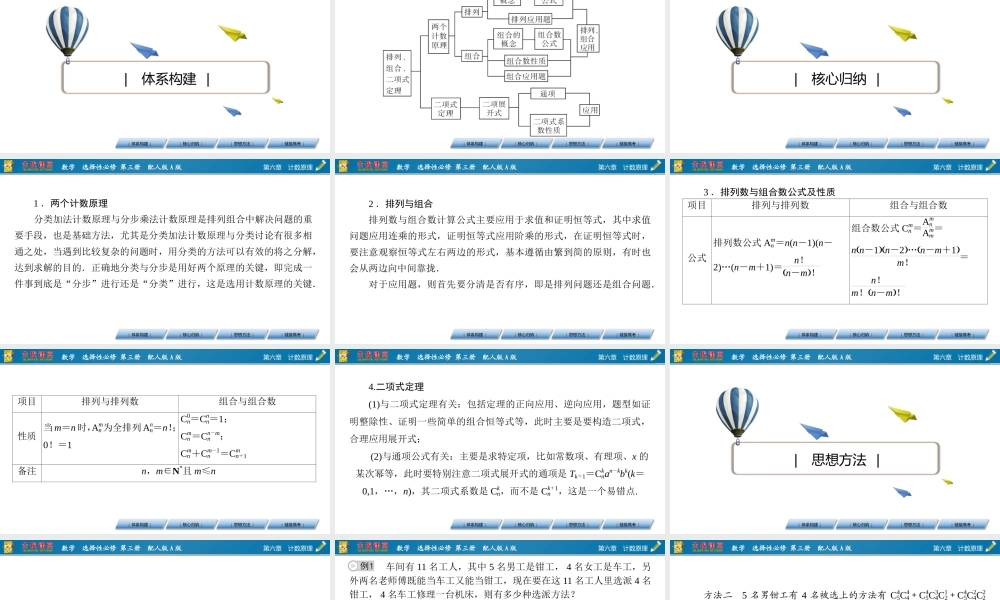
第六章计数原理章末素养提升第六章计数原理数学选择性必修第三册配人版A版|核心归纳||思想方法||链接高考||体系构建||体系构建|第六章计数原理数学选择性必修第三册配人版A版|核心归纳||思想方法||链接高考||体系构建|第六章计数原理数学选择性必修第三册配人版A版|核心归纳||思想方法||链接高考||体系构建||核心归纳|第六章计数原理数学选择性必修第三册配人版A版|核心归纳||思想方法||链接高考||体系构建|1.两个计数原理分类加法计数原理与分步乘法计数原理是排列组合中解决问题的重要手段,也是基础方法,尤其是分类加法计数原理与分类讨论有很多相通之处,当遇到比较复杂的问题时,用分类的方法可以有效的将之分解,达到求解的目的.正确地分类与分步是用好两个原理的关键,即完成一件事到底是“分步”进行还是“分类”进行,这是选用计数原理的关键.第六章计数原理数学选择性必修第三册配人版A版|核心归纳||思想方法||链接高考||体系构建|2.排列与组合排列数与组合数计算公式主要应用于求值和证明恒等式,其中求值问题应用连乘的形式,证明恒等式应用阶乘的形式,在证明恒等式时,要注意观察恒等式左右两边的形式,基本遵循由繁到简的原则,有时也会从两边向中间靠拢.对于应用题,则首先要分清是否有序,即是排列问题还是组合问题.第六章计数原理数学选择性必修第三册配人版A版|核心归纳||思想方法||链接高考||体系构建|3.排列数与组合数公式及性质项目排列与排列数组合与组合数公式排列数公式Amn=n(n-1)(n-2)…(n-m+1)=n!n-m!组合数公式Cmn=AmnAmm=nn-1n-2…n-m+1m!=n!m!n-m!第六章计数原理数学选择性必修第三册配人版A版|核心归纳||思想方法||链接高考||体系构建|项目排列与排列数组合与组合数性质当m=n时,Amn为全排列Ann=n!;0!=1C0n=Cnn=1;Cmn=Cn-mn;Cmn+Cm-1n=Cmn+1备注n,m∈N*且m≤n第六章计数原理数学选择性必修第三册配人版A版|核心归纳||思想方法||链接高考||体系构建|4.二项式定理(1)与二项式定理有关:包括定理的正向应用、逆向应用,题型如证明整除性、证明一些简单的组合恒等式等,此时主要是要构造二项式,合理应用展开式;(2)与通项公式有关:主要是求特定项,比如常数项、有理项、x的某次幂等,此时要特别注意二项式展开式的通项是Tk+1=Cknan-kbk(k=0,1,…,n),其二项式系数是Ckn,而不是Ck+1n,这是一个易错点.第六章计数原理数学选择性必修第三册...