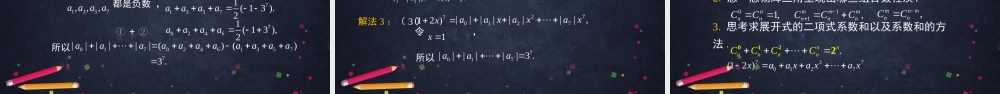0609高二数学（选修-人教B版）-二项式定理（2）-2PPT.pptxVIP免费

二项式定理（2）高二年级数学主讲人：李新国北京市铁路第二中学复习：二项式定理：().nnnnnrrrnnnnnnnabaababCCCCbbCa101222()nN其中各项系数叫做展开式的二项式系数.(,,,)rnCrn01若设，则,abx1().nnnnnnnxCCxCxCx01221通项是展开式的第项.r1(),rnrrrnrnrTCabn10NN,,≤≤121……………………1()ab2()ab3()ab4()ab5()ab11133114641151010516()ab1615201561………………………………………………………………………………………前面的二项式系数表称为“杨辉三角”或“贾宪三角”.杨辉是我国宋朝数学家,他于1261年著《详解九章算法》，在其中详细列出了这样一张图表（见右图），并且指出这个方法出自于更早时期贾宪的著作《黄帝九章算法细草》.在欧洲一般认为这是帕斯卡（Pascal）于1654年发现的，称这个图形为“帕斯卡三角”.1()ab2()ab3()ab4()ab5()ab11121133114641151010516()ab1615201561……1.01nnnCCmnmnnCC2.11mmmnnnCCC3.如果二项式的幂指数n是偶数，那么其展开式中间一项项的二项式系数最大；12nT如果二项式的幂指数n是奇数，那么其展开式中间两项和项的二项式系数相等且最大.12nT112nT和最大，12nnC12nnC2nnC最大，例如n=6时，最大，第4项二项式系数最大，36C例如n=5时，最大，所以第3项和第4项二项式系数最大.2355CC二项式定理：().nnnnnrrrnnnnnnnabaababCCCCbbCa101222二项展开式的二项式系数：,,,,,,.rnnnnnnCCCCC012可以看成以r为自变量的函数(),rnfrC定义域是.{0,1,2,,}n分析：两个数比大小的方法(1)作差法（2）作商法!,!()!rnnCrnr1!,(1)!(1)!rnnCrnr1!(1)!(1)!!()!!rnrnCnrnrCrnrn1!,(1)!(1)!rnnCrnr1!(1)!(1)!!()!!rnrnCnrnrCrnrn对任意的r,r=1,2,…,n-1,n>2.1,nrr1,rnr111111rnrnrnrnCnrCrCrCnr≥≥1212nrnr≤≥1122nnr≤≤如果二项式的幂指数n是偶数，则.2nr=如果二项式的幂指数n是奇数，则或.12nr=12nr=5n6n3r52r36C2355CC4.二项展开式的二项式系数的和等于2.n().nnnnnnnxCCxCxCx01221若再设，则x1.nnnnnnCCCC0122().nnnnnnnnnnabaababCCCCb122012().nnnnnnCCCC...