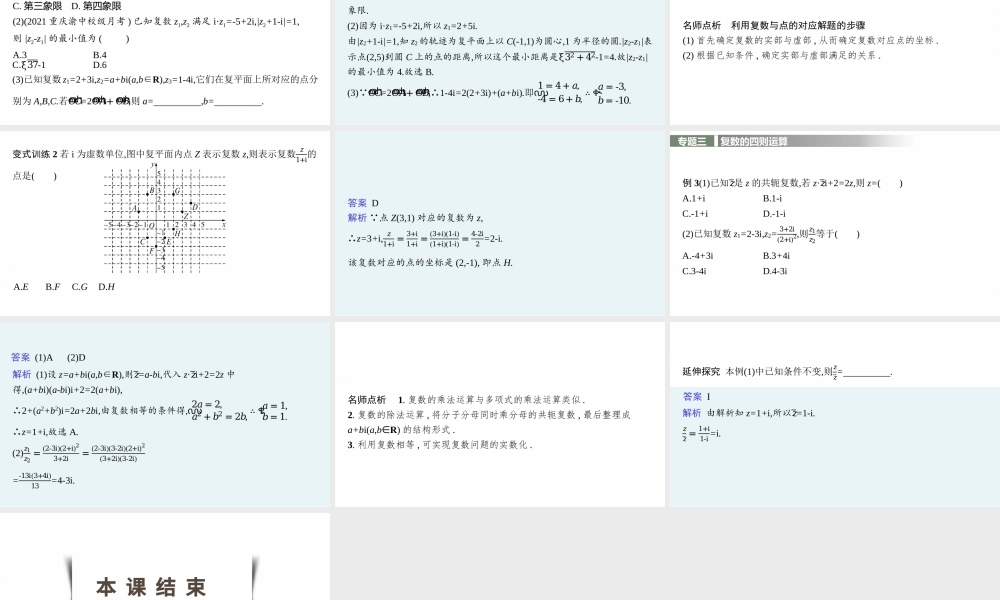
高中同步学案优化设计GAOZHONGTONGBUXUEANYOUHUASHEJI章末整合第2章2022内容索引0102知识网络整合构建专题归纳思维深化知识网络整合构建专题归纳思维深化专题一复数的概念例1当复数z=a2-2a+(a2-3a+2)i满足以下条件时,求实数a的值或取值范围.(1)实数;(2)纯虚数;(3)对应的点在第一象限;(4)对应的点在直线x-y=0上.解(1)z∈R⇔a2-3a+2=0,解得a=1或a=2.(2)z为纯虚数,则ቊ𝑎2-2𝑎=0,𝑎2-3𝑎+2≠0,即ቊ𝑎=0,或𝑎=2,𝑎≠1,且𝑎≠2.故a=0.(3)z对应的点在第一象限,则ቊ𝑎2-2𝑎>0,𝑎2-3𝑎+2>0,∴ቊ𝑎<0,或𝑎>2,𝑎<1,或𝑎>2.∴a<0,或a>2.∴a的取值范围是(-∞,0)∪(2,+∞).(4)依题设(a2-2a)-(a2-3a+2)=0,∴a=2.名师点析处理复数概念问题的两个注意点(1)当复数不是a+bi(a,b∈R)的形式时,要通过变形化为a+bi(a,b∈R)的形式,以便确定其实部和虚部.(2)求解时,要注意实部和虚部本身对变量的要求,否则容易产生增根.变式训练1(1)若复数z=1+i(i为虚数单位),𝑧是z的共轭复数,则z2+𝑧2的虚部为()A.0B.-1C.1D.-2(2)设i是虚数单位,若复数a-103-i(a∈R)是纯虚数,则a的值为()A.-3B.-1C.1D.3答案(1)A(2)D解析(1)因为z=1+i,所以𝑧=1-i,所以z2+𝑧2=(1+i)2+(1-i)2=2i+(-2i)=0.故选A.(2)因为a-103-i=a-10(3+i)(3-i)(3+i)=a-10(3+i)10=(a-3)-i,由纯虚数的定义,知a-3=0,所以a=3.专题二复数的几何意义例2(1)在复平面内,复数-2+3i3-4i(i是虚数单位)所对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限(2)(2021重庆渝中校级月考)已知复数z1,z2满足i·z1=-5+2i,|z2+1-i|=1,则|z2-z1|的最小值为()A.3B.4C.ξ37-1D.6(3)已知复数z1=2+3i,z2=a+bi(a,b∈R),z3=1-4i,它们在复平面上所对应的点分别为A,B,C.若𝑂𝐶ሬሬሬሬሬԦ=2𝑂𝐴ሬሬሬሬሬԦ+𝑂𝐵ሬሬሬሬሬԦ,则a=,b=.答案(1)B(2)B(3)-3-10解析(1)-2+3i3-4i=(-2+3i)(3+4i)25=-18+i25=-1825+125i,故复数-2+3i3-4i对应的点位于第二象限.(2)因为i·z1=-5+2i,所以z1=2+5i.由|z2+1-i|=1,知z2的轨迹为复平面上以C(-1,1)为圆心,1为半径的圆.|z2-z1|表示点(2,5)到圆C上的点的距离,所以这个最小距离是ξ32+42-1=4.故|z2-z1|的最小值为4.故选B.(3) 𝑂𝐶ሬሬሬሬሬԦ=2𝑂𝐴ሬሬሬሬሬԦ+𝑂𝐵ሬሬሬሬሬԦ,∴1-4i=2(2+3i)+(a+bi).即൜1=4+𝑎,-4=6+𝑏,∴ቊ𝑎=-3,𝑏=-10.名师点析利用复数与点的对应解题的步骤(1)首先确定复数的实部与虚部,从而确定复数对应点的坐标.(2)根据已知条件,确定实部与虚部满足的关系.变式训练2若i为虚数单位,图中复平面内...