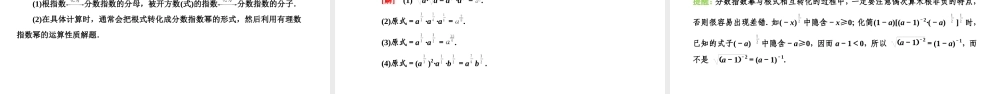4.1 指数k1gr4.pptxVIP免费

第四章指数函数与对数函数4．1指数明确目标发展素养1.根据具体实例，了解指数的拓展过程．2.理解根式的性质，会进行简单的n次方根的运算．3.理解分数指数幂的意义及分数指数幂与根式的互化．4.掌握指数的运算性质，会利用整体代换的思想求值.1.借助n次方根及根式的概念，分数指数幂的含义，提升数学抽象素养．2.通过分数指数幂、运算性质的推导，培养逻辑推理素养．3.借助指数幂的运算性质对代数式化简或求值，培养数学运算素养.知识点一根式的概念及其性质(一)教材梳理填空1．n次方根的概念：定义一般地，如果xn＝a，那么___叫做a的，其中n＞1，且n∈N*个数n是奇数a＞0x＞0x仅有一个值，记为____a＜0x＜0n是偶数a＞0x有两个值，且互为相反数，记为____a＜0x不存在xn次方根na±na[微思考]为什么负数没有偶次方根？提示：因为正数和负数的偶次方都是正数，故逆运算求偶次方根时，负数没有偶次方根．2．根式：(1)定义：式子叫做根式，这里n叫做，a叫做.(2)性质：①(na)n＝(n＞1，且n∈N*)．②当n为奇数时，nan＝___；当n为偶数时，nan＝|a|＝___________.[微思考](na)n中实数a的取值范围是任意实数吗？提示：不一定，当n为大于1的奇数时，a∈R；当n为大于1的偶数时，a≥0.aa，a≥0，－a，a＜0根指数被开方数naa(二)基本知能小试1．判断正误：(1)任意实数的奇次方根只有1个．()(2)正数的偶次方根有两个且互为相反数．()(3)1－π2＝1－π.()答案：(1)√(2)√(3)×2．若a是实数，则下列式子中可能没有意义的是()A.4a2B.5aC.5－aD.4a答案：D3．化简x＋32－3x－33得________．答案：6或－2x解析：当a＜0时，a的偶次方根无意义．解析：原式＝|x＋3|－(x－3)，当x≥－3时，原式＝6；当x<－3时，原式＝－2x.知识点二分数指数幂的意义(一)教材梳理填空分数指数幂正分数指数幂规定：amn＝(a＞0，m，n∈N*，n＞1)负分数指数幂规定：amn＝＝____(a＞0，m，n∈N*，n＞1)性质0的正分数指数幂等于,0的负分数指数幂nam0没有意义[微思考]在分数指数幂与根式的互化公式amn＝nam中，为什么必须规定a>0?提示：①若a＝0,0的正分数指数幂恒等于0，即nam＝amn＝0，无研究价值．②若a<0，amn＝nam不一定成立，如(－2)32＝2－23无意义，故为了避免上述情况规定了a>0.(二)基本知能小试1．填表，用分数指数幂的形式表示下列各式(a＞0)：a2a1a3aa_____________2．323可化为()A.2B.3C.39D.9答案：C知识点三有理数指数幂与无理数指数幂(一)教材梳理填空...