1.3.1-2iw4aj.pptVIP免费

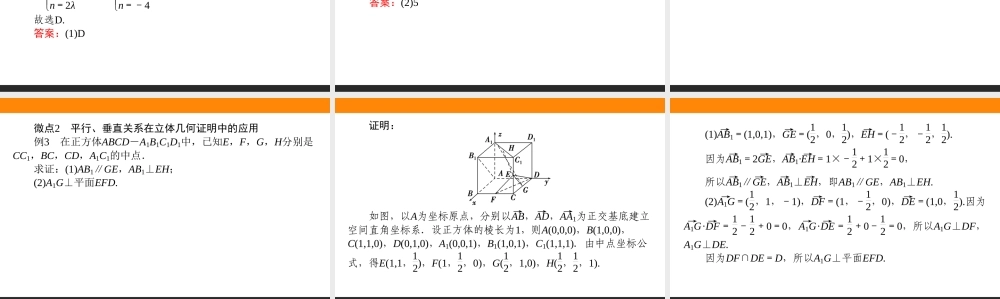
1.3.1空间直角坐标系1.3.2空间向量运算的坐标表示[教材要点]要点一空间直角坐标系如果空间的一个基底中的三个基向量两两垂直，且长度都为1，那么这个基底叫做______________．在空间直角坐标系Oxyz中，给定向量a，由空间向量基本定理，存在唯一的有序实数组(x，y，z)使a＝xi＋yj＋zk，有序实数组(x，y，z)叫做a在空间直角坐标系Oxyz中的坐标，记作a＝________.单位正交基底(x，y，z)要点二空间向量的坐标表示在空间选定一点O和一个单位正交基底{i，j，k}．以点O为原点，分别以i，j，k的方向为正方向，以它们的长为单位长度建立三条数轴：x轴、y轴、z轴，它们叫做坐标轴．这时我们就建立了一个空间直角坐标系Oxyz，O叫做原点，i，j，k叫做________，通过每两个坐标轴的平面叫做坐标平面．在空间直角坐标系中，让右手拇指指向x轴的方向，食指指向y轴的方向，如果中指指向z轴的方向，则称这个坐标系为______________．坐标向量右手直角坐标系要点三空间向量运算的坐标表示设a＝(a1，a2，a3)，b＝(b1，b2，b3)，空间向量的坐标运算法则如下：运算坐标表示加法a＋b＝_______________________减法a－b＝_______________________数乘λa＝_______________________数量积a·b＝_______________________(a1＋b1，a2＋b2，a3＋b3)(a1－b1，a2－b2，a3－b3)(λa1，λa2，λa3)，λ∈Ra1b1＋a2b2＋a3b3要点四空间向量的平行、垂直、模、夹角公式与两点间的距离公式设a＝(a1，a2，a3)，b＝(b1，b2，b3)，则平行(a∥b)a∥b(b≠0)⇔a＝λb⇔________垂直(a⊥b)a⊥b⇔a·b＝0⇔______________________(a，b均为非零向量)模|a|＝a·a＝________________a1＝λb1a2＝λb2a3＝λb3(λ∈R)a1b1＋a2b2＋a3b3＝0a21＋a22＋a23夹角公式cos〈a，b〉＝a·b|a|·|b|＝a1b1＋a2b2＋a3b3a21＋a22＋a23b21＋b22＋b23两点间的距离公式设P1(x1，y1，z1)，P2(x2，y2，z2)则dP1P2＝P1P2＝|P1P2→|＝________________x2－x12＋y2－y12＋z2－z12[基础自测]1．判断正误(正确的画“√”，错误的画“×”)(1)对于空间任意两个向量a＝(a1，a2，a3)，b＝(b1，b2，b3)，若a与b共线，则a1b1＝a2b2＝a3b3.()(2)若向量AB→＝(x1，y1，z1)，则点B的坐标为(x1，y1，z1)．()(3)“两向量同向”是“两向量平行”的充分不必要条件．()(4)空间向量的加法、减法、乘法坐标运算的结果依然是一个向量．()××√×2．已知向量a＝(3，－2,1)，b＝(－2,4,0)，则4a＋2b等于()A．(16,0,4)...