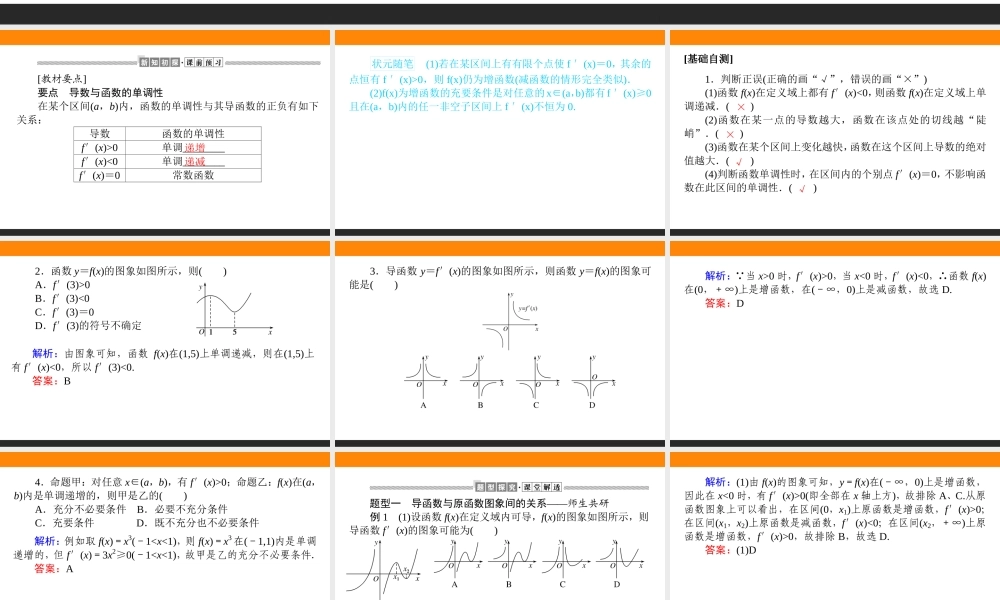
第1课时函数的单调性与导数[教材要点]要点导数与函数的单调性在某个区间(a,b)内,函数的单调性与其导函数的正负有如下关系:导数函数的单调性f′(x)>0单调________f′(x)<0单调________f′(x)=0常数函数递增递减状元随笔(1)若在某区间上有有限个点使f′(x)=0,其余的点恒有f′(x)>0,则f(x)仍为增函数(减函数的情形完全类似).(2)f(x)为增函数的充要条件是对任意的x∈(a,b)都有f′(x)≥0且在(a,b)内的任一非空子区间上f′(x)不恒为0.[基础自测]1.判断正误(正确的画“√”,错误的画“×”)(1)函数f(x)在定义域上都有f′(x)<0,则函数f(x)在定义域上单调递减.()(2)函数在某一点的导数越大,函数在该点处的切线越“陡峭”.()(3)函数在某个区间上变化越快,函数在这个区间上导数的绝对值越大.()(4)判断函数单调性时,在区间内的个别点f′(x)=0,不影响函数在此区间的单调性.()××√√2.函数y=f(x)的图象如图所示,则()A.f′(3)>0B.f′(3)<0C.f′(3)=0D.f′(3)的符号不确定解析:由图象可知,函数f(x)在(1,5)上单调递减,则在(1,5)上有f′(x)<0,所以f′(3)<0.答案:B3.导函数y=f′(x)的图象如图所示,则函数y=f(x)的图象可能是()解析: 当x>0时,f′(x)>0,当x<0时,f′(x)<0,∴函数f(x)在(0,+∞)上是增函数,在(-∞,0)上是减函数,故选D.答案:D4.命题甲:对任意x∈(a,b),有f′(x)>0;命题乙:f(x)在(a,b)内是单调递增的,则甲是乙的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析:例如取f(x)=x3(-10(即全部在x轴上方),故排除A、C.从原函数图象上可以看出,在区间(0,x1)上原函数是增函数,f′(x)>0;在区间(x1,x2)上原函数是减函数,f′(x)<0;在区间(x2,+∞)上原函数是增函数,f′(x)>0,故排除B,故选D.答案:(1)D(2)(多选题)设f′(x)是函数f(x)的导函数,将y=f(x)和y=f′(x)的图象画在同一个平面直角坐标系中,正确的是()解析:(2)A,B,C均有可能;对于D,若C1为导函数,则y=f(x)应为增函数,不符合;若C2为导函数,则y=f(x)应为减函数,...