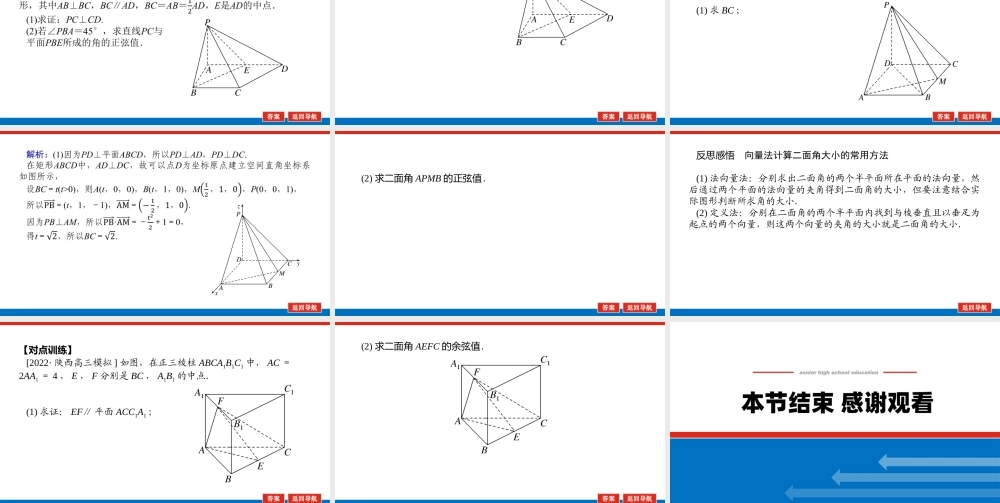
第1课时利用空间向量求空间角关键能力—考点突破关键能力—考点突破答案:D答案:C反思感悟用向量法求异面直线所成角的一般步骤(1)选择三条两两垂直的直线建立空间直角坐标系.(2)确定异面直线上两个点的坐标,从而确定异面直线的方向向量.(3)利用向量的夹角公式求出向量夹角的余弦值.(4)两异面直线所成角的余弦值等于两向量夹角余弦值的绝对值.[提醒]注意向量的夹角与异面直线所成的角的区别:当异面直线的方向向量的夹角为锐角或直角时,就是此异面直线所成的角;当异面直线的方向向量的夹角为钝角时,其补角才是异面直线所成的角.(2)求直线AN与平面PDM所成角的正弦值.(2)若∠PBA=45°,求直线PC与平面PBE所成的角的正弦值.考点三二面角[综合性][例2][2021·全国乙卷]如图,四棱锥P-ABCD的底面是矩形,PD⊥底面ABCD,PD=DC=1,M为BC的中点,且PB⊥AM.(1)求BC;(2)求二面角APMB的正弦值.反思感悟向量法计算二面角大小的常用方法(1)法向量法:分别求出二面角的两个半平面所在平面的法向量,然后通过两个平面的法向量的夹角得到二面角的大小,但要注意结合实际图形判断所求角的大小.(2)定义法:分别在二面角的两个半平面内找到与棱垂直且以垂足为起点的两个向量,则这两个向量的夹角的大小就是二面角的大小.【对点训练】[2022·陕西高三模拟]如图,在正三棱柱ABCA1B1C1中,AC=2AA1=4,E,F分别是BC,A1B1的中点.(1)求证:EF∥平面ACC1A1;(2)求二面角AEFC的余弦值.