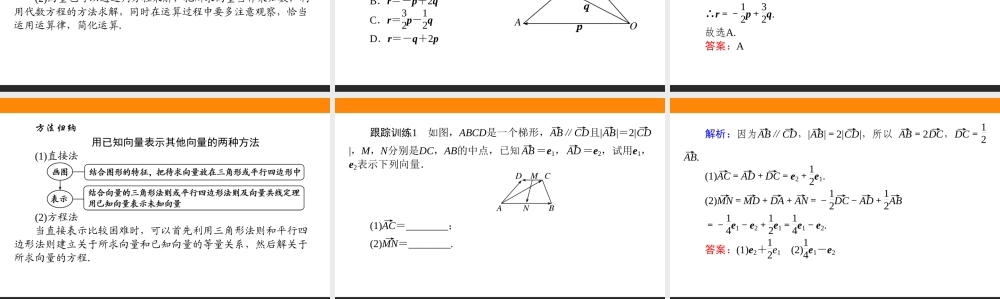
6.2.3向量的数乘运算最新课标1.通过实例分析,掌握平面向量的数乘运算及其运算规则,理解其几何意义.2.了解平面向量的线性运算性质及其几何意义.3.掌握向量共线定理及其证明过程,会根据向量共线定理判断两个向量是否共线.[教材要点]要点一向量数乘运算1.向量的数乘的定义实数λ与向量a的积是一个________,这种运算叫做向量的________,记作________,它的长度与方向规定如下:(1)|λa|=|λ||a|.(2)当λ>0时,λa的方向与a的方向________;当λ<0时,λa的方向与a的方向________.(3)当λ=0时,λa=0.向量数乘λa相同相反状元随笔理解数乘向量应注意的问题(1)向量数乘的结果依然是向量,要从长度与方向加以理解.(2)实数与向量可以相乘,但是不能相加、减.如λ+a→,λ-a→均没有意义.2.向量的数乘的几何意义(1)当|λ|>1时,有|λa|>|a|,这意味着表示向量a的有向线段的原方向(λ>1)或反方向(λ<-1)上伸长为原来的|λ|倍;(2)当0<|λ|<1时,有|λa|<|a|,这意味着表示向量a的有向线段在原方向(0<λ<1)或反方向(-1<λ<0)上缩短为原来的|λ|倍.3.向量的数乘的运算律设λ,μ为实数,那么(1)结合律:λ(μa)=________________;(2)第一分配律:(λ+μ)a=________________;(3)第二分配律:λ(a+b)=________________.特别地,我们有(-λ)a=-(λa)=λ(-a),λ(a-b)=λa-λb.(λμ)aλa+μaλa+λb状元随笔(1)对于非零向量a→,当λ=1|a→|时,λa→表示a→方向上的单位向量.(2)向量的数乘运算类似于代数多项式的运算.主要是“合并同类项”“提取公因式”,但这里的“同类项”及“公因式”指的是向量,实数指的是向量的系数.要点二共线向量定理向量a(a≠0)与b共线,当且仅当有唯一一个实数λ,使________.b=λa状元随笔向量共线定理的理解注意点及主要应用(1)定理中a→≠0→不能漏掉.若a→=b→=0→,则实数λ可以是任意实数;若a→=0→,b→≠0→,则不存在实数λ,使得b→=λa→.(2)这个定理可以用一般形式给出:若存在不全为0的一对实数t,s,使ta→+sb→=0→,则a→与b→共线;若两个非零向量a→与b→不共线,且ta→+sb→=0→,则必有t=s=0.[教材答疑]教材P14思考如果把非零向量a的长度伸长到原来的3.5倍,方向不变得到向量b,向量b该如何表示?向量a,b之间的关系怎样?提示:b=3.5a,a与b共线.[基础自测]1.判断正误(正确的画“√”,错误的画“×”)(1)实数λ与向量a的积还是向量.()(2)对于非...